QAOA or Quantum Approximation Optimization Algorithm is one of the most promising algorithms showing Quantum supremacy which can be implemented on the near term quantum computers. Being an approximation algorithm, it does not give the best result but gives a result which is ‘good enough’ and the accuracy governed by the lower bound of the approximation ratio.
Here we will understand the working of QAOA with an apt example taking the MAXCUT problem.
Understanding the problem statement:
Basically in QAOA we are given a n bit string Z=Z₁Z₂…Zn , Zᴋ∈ {0,1}ⁿ and m clauses and the aim is to maximize a given objective/cost function C=∑Cᴋ(z) where the summation goes from ᴋ=1 to m and Cᴍ ∈{0,1} which queries string Z and checks if a given substring satisfies a certain property. We have to maximize for a given Z given 2ⁿ given possibilities. The most trivial solution will be to query each z which would be needing O(2ⁿ) queries. There is no exact solution for the same but there are some approximation solutions and we will look at a quantum approximation solution which gives good result in detail.
In the Quantum approximation algorithm we will take the objective function C as an operator.
here we can see that C has eigenvectors |z> and eigenvalues ∑Cᴋ(z) =f(z) for each |z>. Our aim is to find the maximum eigenvalue which we denote by f(z’) corresponding to Cᴍᴀx. For a given arbitrary state |z> we can create a superposition of states with coefficients Aᴢ where the complete state is |ψ> given by ∑Aᴢ|z〉such that ∑|Aᴢ|²= 1. Given the superstition state |ψ> we can find the expectation value of the C operator which is <C> = <ψ|C|ψ>.
Given , |ψ> = |z>, we get <C> = <z|C|z> = f(z), which can be calculated classically if z is known but we don’t know the value of z for which would maximize <C>. The answer is to find a state |ψ> which would maximize <C> as a solution for finding a |z> which will maximize C(z).

Here we see that <C>ᴍᴀx=f(z’) happens only when |ψ> = |z’>. So the explanation for this would be if we maximize and get <C>ᴍᴀx, it would be equivalent to measuring the state |ψ> in |z> basis and getting |z’> with probability 1. But we can’t exactly get <C>ᴍᴀx and only get a <C> which is closer to this.
The solution is to find a |ψ> which is a superposition of |z>, the probability of finding |z’> being |A’z|², and hopefully the probability is so high that if we measure Ψ many times we would get |z’>. But, Later we can see that in general|A′z|² is so small that we can only hope to find a|z〉that makes C(z) close to C(z′).
Let’s take an example state |ψ> which is a superposition of |z> basis states:

When we measure it many times we get a distribution of basis states with expectation values C(z) and maximum value being C(z’) for the state |z’>.
We can see that the average of the distribution is :

In the above given state the probability for obtaining a given state and even the state |z’> is 1/2ⁿ as it is uniformly distributed.
Thus we see that the |ψ> state is not interesting enough but we can rotate this state to make it closer to |z’>. And thus we introduce two kinds of rotations U(C,γ) which is equivalent to e^(-iγC) and U(B,β) which is equivalent to e^(-iβB).
Let’s talk about these two rotations next:
U(C,γ):
The rotation is defined as:

Here we are using a phase gate which is based on constraint that for certain |z>, a phase e^(-iγ) is added to |z> for each of the satisfied condition Cα.

Here we see that if the value of Cα=1 or the condition is satisfied, we multiply the superpositioned state with a phase gate e^(-iγ) or else if the condition is not satisfied or Cα is 0, the respective state stays the same. Sometimes an ancilla qubit is required depending on the C causes.
Let’s take an example, suppose we have a state |ψ> = |x₁> |x₂> |x₃>, where n=3 and taking a general state we have |x₁> = α₀|0>+α₁|1> , |x₂> = β₀|0>+β₁|1> and |x₃> = γ₀|0>+γ₁|1>, and we have three clauses with it.
C₁ = 1 , if x1=1 , C₂=1 if x1=x2=1 , C₃=1 if x1=x2=x3=1.
this gives us the respective truth table C₁(000)=0,C₁(001)=0,C₁(010)=0,C₁(011)=0,C₁(100)=1,C₁(101)=1,C₁(110)=1,C₁(111)=1 and C₂(000)=0,C₂(001)=0,C₂(010)=0,C₂(011)=0,C₂(100)=0,C₂(101)=0,C₂(110)=1,C₂(111)=1 and C₃(000)=0,C₃(001)=0,C₃(010)=0,C₃(011)=0,C₃(100)=0,C₃(101)=0,C₃(110)=0,C₃(111)=1.
|x1x2x3>→α0β0γ0|000>+α0β0γ1|001>+α0β1γ0|010>+α0β1γ1|011>+R(γ)α1β0γ0|100>+R(γ)α1β0γ1|101>+R²(γ)α1β1γ0|110>+R³(γ)α1β1γ1|111>.
Phase change alone doesn’t change the probability of obtaining a certain basis as |Rᵐ⁽ᶻ⁾Az|=e^(-im(z)γ).e^(im(z)γ)|Az|² = |Az|². So there is a need for introduction of a rotation operator U(B,β).
U(B,β):
In this rotation operator we define B as:

Now we define the β dependent product of commuting one bit operators:

The decomposition of B is exact because the operators are commuting.
We have a rotation operator as Rx(θ)=e^(iθ/2σˣ), where
θ ∈ [0, 2π]. We can use this to make U(B,β).

We have 2β ∈ [0,2π] → β ∈ [0,π]. This can be easily done with depth 1 without the need of any control ancillary bits like the previous Unitary operator for certain causes.

It is not certain that even after we apply the above operators once |ψ’> = U(C,γ)U(B,β)|ψ> is close enough to |z’>. We have to apply both the operations multiple times , with different β and γ each time. On applying it p times we get a state which depends on the angles and is defined as:

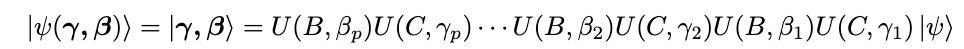
where γ = (γ1,γ2,··· ,γp) and β = (β1,β2,··· ,βp). It is not easy to determine the right angles in advance and it requires 2p-dimensional optimization to find the optimal angle with many iterations.
Applying QAOA to MAXCUT:
Maxcut problem is defined in such a way that given a graph (V,E), the problem is to partition the nodes of a graph into two sets such that the number of edges connecting nodes in opposite sets is maximized. The nodes or vertices can be represented in such a way that we have a string of n bits where each bit can have a value of 0 or 1. The total number of partitionings we can have are 2ⁿ.
Let’s say we have a connected graph of n vertices and edge set being {jk} of size m. We can classify each vertex into a set of two by giving values g(i)=1 or g(i)=-1, where g(i) is a function which tells if a vertex belongs to one partition or the other.
We define that a cut occurs when g(i)g(j)=-1. We need to find a cut where we have the maximum number of disagreement of the set {jk}. The true maximum can be less than m.
Our objective function thus is C = ∑ Cᴊᴋ where <jk> is an edge.
where,
Cᴊᴋ=1/2(-g(i)g(j) + 1) = {0,1}
Cᴊᴋ is 0 when g(i)g(j)=1 means both the vertices are in the same partition, while it is 1 when g(i)g(j)=-1 shows both the vertices are in different partitions means there is a cut.
We can translate this objective function in the quantum perspective by treating all the vertices as n qubits in the computational basis such that the vertices can be classified as |0> or |1>. Thus the 2^n partitionings are classified as the 2^n computational basis formed by creating the superposition of |0>ⁿ. The objective function is translated as an operator:
C|z> = ∑ Cᴊᴋ(z)|z> = C(z)|z>
where,
Cᴊᴋ|z> = 1/2(-gⱼ⊗ gᴋ + I)|z>
such that if there is a cut then gⱼ⊗ gᴋ =-I and zj and zk are both |0> or |1> if there is no cut then we have gⱼ⊗ gᴋ = I , they belong to different qubits. Thus we get either |z> or 0 correspondingly.
Since we want the output to be either |z> or 0, the best bet for the objective function will be σᶻ as it gives σᶻ|0> = +1 and σᶻ|1> = -1. Thus we will get gⱼ⊗ gᴋ to be -I or I.
Thus Cᴊᴋ=1/2(gⱼ⊗ gᴋ + I ) = 1/2 (σᶻⱼ⊗ σᶻᴋ + I).
Now we construct U(B,β) and U(C,γ):
U(C,γ)=e^(-iγC) = e^(-iγ∑Cᴊᴋ)=∏e^(-iγCᴊᴋ)= ∏ U(Cᴊᴋ,γ)
U(Cᴊᴋ,γ)=e^(-iγ.1/2(-σᶻⱼ⊗σᶻ ᴋ+ I) = e^(-iγ/2(σᶻⱼ⊗σᶻᴋ).e^(-iγ/2I)
So we get two circuits for the first part which can be implemented with CNOT and R(-γ) and the second part with e^(-iγ/2I) being a phase change gate with angle = -γ/2. The circuit can be shown as:

When we take a two qubit system to represent a 4 vertices graph and apply the above U(C,γ) we see that a phase e^(iγ) is added when both the vertices are different which represents a cut.
The operator U(B,β) is same as we discussed above and the workflow will be the same too using parameters optimization for both β and γ to improve the state |ψ>.
Next we will be working on the above Maxcut using QAOA withthe computer library Blueqat and showing the complete workflow with parameters optimization.
References:
- Edward Farhi, Jeffrey Goldstone, and Sam Gutmann. A Quantum Approximate Optimization Algorithm. arXiv1411.4028.
- Zhihui Wang, Stuart Hadfield, Zhang Jiang, and Eleanor G. Rieffel. Quantum approximate optimization algorithm for MaxCut: A fermionic view. Phys. Rev. A, 97(2):1–13, 2018.
- https://www.cs.umd.edu/class/fall2018/cmsc657/projects/group_16.pdf
- Edward Farhi. Quantum Supremacy through the Quantum Approximate Optimization Algorithm. arXiv Prepr.arXiv1602.07674

