こんにちは、リュードベリ原子型の新型量子コンピュータが2022年に提供が開始予定です。NasdaqなどはAtom Computingなどの原子型企業の調達をお祝いするような広告もうっており、イオントラップ型の次の新型として今年注目されています。
さて、個人的にQuEraの論文がクオリティが高く、リュードベリ原子型の量子コンピュータの概要が分かりやすいので、紹介してきました。今回は二種類のパラメータを変化させたQAOAと呼ばれる量子コンピュータのアルゴリズムの実行の論文を見てみます。
QAOAは量子コンピュータを使って行われる近似アルゴリズムで、量子断熱計算と呼ばれる理論をもとに、段階的に量子状態を変化させる量子断熱計算をベースに離散最適化問題を定式化したイジングモデルの問題を解くというものです。今回は量子シミュレータと呼ばれる原子の仕組みを応用して原子の動きを使って離散最適化・グラフ問題を解くものを見てみます。
リュードベリ原子型量子コンピュータは、基底状態というエネルギーの低い状態と、リュードベリ状態と呼ばれる電子が原子核から遠く離れた状態を使いこなすことができるマシンです。リュードベリ原子はリュードベリ半径と呼ばれる一定半径内での特徴的な電子のふるまいを活用し、ほかの原子との相互作用においてリュードベリブロッケードと呼ばれる複数の電子が共存できない相互作用を持っています。このリュードベリ状態を活用したエネルギーの状態はハミルトニアンと呼ばれる演算子によって記述ができ、量子シミュレータはこのハミルトニアンの制約の下で原子のシミュレーションが行えます。
2022年の初頭段階で最大289量子ビットのQAOAを行った論文がでています。
論文:
Quantum Optimization of Maximum Independent Set using Rydberg Atom Arrays
S. Ebadi1,∗ , A. Keesling1,2,∗ , M. Cain1,∗ , T. T. Wang1 , H. Levine1,‡ , D. Bluvstein1 , G. Semeghini1 , A. Omran1,2 , J.-G. Liu1,2 , R. Samajdar1 , X.-Z. Luo2,3,4 , B. Nash5 , X. Gao1 , B. Barak5 , E. Farhi6,7 , S. Sachdev1,8 , N. Gemelke2 , L. Zhou1,9 , S. Choi7 , H. Pichler10,11, S.-T. Wang2 , M. Greiner1,† , V. Vuletic´ 12,† , M. D. Lukin1,† 1Department of Physics, Harvard University, Cambridge, MA 02138, USA 2 QuEra Computing Inc., Boston, MA 02135, USA 3Department of Physics and Astronomy, University of Waterloo, Waterloo N2L 3G1, Canada 4Perimeter Institute for Theoretical Physics, Waterloo, Ontario N2L 2Y5, Canada 5 School of Engineering and Applied Science, Harvard University, Cambridge, MA 02138, USA 6Google Quantum AI, Venice, CA 90291 7Center for Theoretical Physics, Massachusetts Institute of Technology,Cambridge, MA 02139 8 School of Natural Sciences, Institute for Advanced Study, Princeton, NJ 08540, USA 9Walter Burke Institute for Theoretical Physics, California Institute of Technology, Pasadena, CA 91125 10Institute for Theoretical Physics, University of Innsbruck, Innsbruck A-6020, Austria 11Institute for Quantum Optics and Quantum Information, Austrian Academy of Sciences, Innsbruck A-6020, Austria 12Department of Physics and Research Laboratory of Electronics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA ∗ These authors contributed equally to this work ‡ Current affiliation: AWS Center for Quantum Computing, Pasadena, CA 91125 † Corresponding authors
https://arxiv.org/pdf/2202.09372.pdf
概略は、組合せ最適化問題を量子コンピュータで解く際の基本的な問題ですが、イジングモデルと呼ばれるモデルに落とし込まれます。
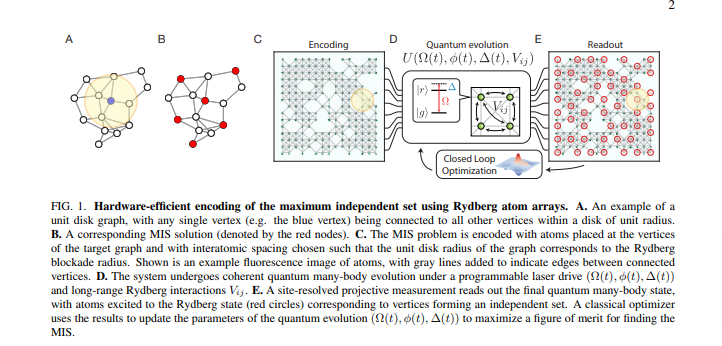
Aは問題をグラフに落とした時の原子一つのリュードベリブロッケードを表していて、この半径内に影響を及ぼします。
Bは実際に問題を解いた際の解で、赤白で量子の|g>,|r>状態がそれぞれ01に対応します。最大独立集合問題をグラフ問題で解いた際の解はこのように表記されます。
Cは問題のエンコーディングで、原子を光ピンセットで止めた後、動的な光ピンセットで原子を並べ替えグラフ問題の形に実際に原子をならべます。
Dは時間発展計算で、一瞬光ピンセットを解除しレーザーを当てて原子の状態を制御します。その際に時間によって変更できるパラメータが3種類あり、距離のパラメータは最初に光ピンセットで設定されているため固定です。
Eは計算結果となっていて、設置されたパラメータから導きされた量子状態が表現されます。
今回は上記の時間発展パラメータを使ってQAOAを行った例を見てみます。
QAOAはこの時間発展計算をやりますが、パラメータを随時更新します。更新の方針は全体のハミルトニアンの期待値が小さくなるように計算します。
引用:https://arxiv.org/pdf/2202.09372.pdf
ハミルトニアンを確認します。こちらのハミルトニアンの構成が重要です。
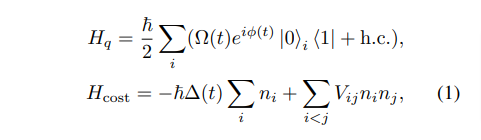
引用:https://arxiv.org/pdf/2202.09372.pdf
QAOAでは二つのハミルトニアンを結合して使います。時間発展の各時間では時間非依存のシュレディンガー方程式の解の重ね合わせとなっていて、
上記のハミルトニアンでは固定された時間tをつかいます。この二つのハミルトニアンの構成は離散最適化では一般的で、上がドライバー、下がコストとよばれます。
ドライバーでは解の探索方法を決め、コストには解きたい問題の問題設定を入れます。
初期の固有状態からスタートし、最終の固有状態に落ち着きます。
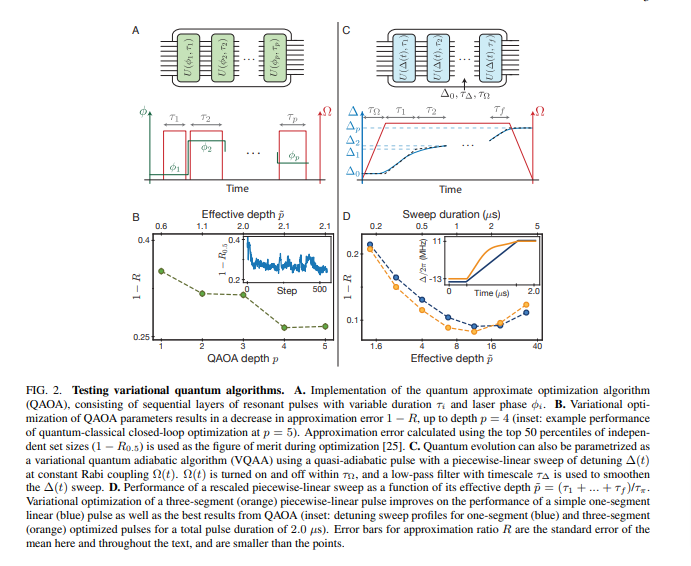
本題の今回の論文の時間発展のパラメータ構成に移ります。今回の論文では時間発展パラメータの変化で二種類行っています。
一つ目が時間τと位相φを設定する、ドライバー側の設定。
二つ目がコスト側のハミルトニアンのバイアス項と、ドライバー側全体にかかるパラメータ制御です。
引用:https://arxiv.org/pdf/2202.09372.pdf
上記を見る限り、面白いですね。Aのほうでは、時間発展のτをかけながら、解除したときにφを変化させて離散的な制御を実現しています。Bの方では、QAOAというよりは、連続的にバイアスを制御しており、ドライバー側は最終的には0になりますが、ほぼ途中は固定値に近いです。VQAAという名前がついてます。すこし量子アニーリングに近いですね。
どちらもおもしろい実験かと思います。ドライバー側のハミルトニアンを見る限りは古典を超えるのは厳しいのではないかとおもいますが、フルプログラマブルを期待します。以上です。
