はじめに
blueqatで量子機械学習をちょっと見てみます。
背景
機械学習を行うというのはとても大事です。量子アニーリングではボルツマンマシンと呼ばれるタイプのものが流行りました。ゲートではそっから少し進んでボルンマシンを使います。
また、量子アニーリングのボルツマンマシンはエラーの多さからうまくいきませんでした。量子ゲートもまだまだエラーが多いので、その辺りも考察します。
まだ厳しそうな雰囲気ありますが、せっかくなのでやってみましょう。
パラメタライズド量子回路
量子ゲートで流行ったVQEやQAOAはAnsatzと呼ばれる量子回路に角度パラメータを導入し、それを古典最適化のアルゴリズムを使って動かすということをしていました。主に扱う問題は固有値問題で、変分原理や量子断熱定理などを使っていましたが、機械学習ではほぼ使わなくて大丈夫そうです。

全体概要
既存機械学習と方向性を合わせます。また、入出力のデータに関してはまだ課題がありますが、その辺りも含めて温度感を見ます。まず、教師あり学習です。
・入力データ(量子回路)とターゲット(古典)
・量子回路のモデル(量子回路)
・測定と期待値(古典)
・損失関数(古典)
・最適化アルゴリズム(古典勾配法)
・ハイパーパラメータ(古典ブラックボックス最適)
こんな感じで進めています。VQE/QAOAなどの固有値ソルバーはUCCansatzやQAOAansatzと呼ばれる量子回路がありましたが、量子機械学習では世間は色々選んでいる最中ですが、ここでは、「テンソルネットワークモデル」を採用します。
今回は量子古典のNNを直列で繋いだり併用はせず、シンプルに量子回路だけでモデルを組み立てます。
入力データ(量子)
こちらは基本量子回路でデータを入力します。一番簡単なのはXゲートを利用してデータを01で入力する方法です。もつれなどを使って効率的なデータ入力なども今後ありそうですが、今回は入力は01にします。

ターゲット(古典)
こちらは量子回路ではないです。最終の計算結果は損失関数を通じて取り出す予定なので、スカラー値を使います。
量子回路のモデル(量子)
これが一番大事です。機械学習でどのようにモデルを学習させるかです。いろんなモデルが提案されていますが、私たちはテンソルネットワークを採用します。
テンソルネットワークの中でも今回は下記の二つを見てみたいと思います。
- MPS
- MERA/TTN
構造が分かりやすくシンプルです。MPSは行列積状態です。回路は、

となります。この二つを学習させてみます。パラメータはこのモデル内に角度として入っています。実際にはRX,RY,RZゲートと、RXX,RYY,RZZゲートなどを使います。CXなど角度の設定のないゲートを使うこともあります。
測定と期待値(古典)
損失関数を求める前に、測定をする必要があります。答えは状態ベクトルに応じて出てきます。今回はZ軸での測定をしました。複数の軸で評価するみたいなのはあるかもしれません。
このあと損失関数にかけずに、このZの期待値を使って最適化をかけるとそのままVQEになります。最適化ができているかなど確認したいときには期待値を戻すようにして経過を見ると確認できます。
損失関数(古典)
上記の期待値と入力に対するターゲットから損失関数を設定します。
で設定をします。これで準備完了です。
最適化計算(古典)
量子回路に微分を仕込んでもいいですが、遅くなるので差分法を使います。モデル内に設定した角度パラメータから微分係数をとり、勾配法を使います。最近は様々なアルゴリズムがありますが、基本的には、学習率eとして、微分係数を使って、
偏微分を考えて更新します。最近はpytorch/tensorflowなどでは自動微分などがありますが、まだ複素数を実装しているところなのでちょっと時間かかりそうだったので今回はblueqatでスクラッチ実装しました。
ハイパーパラメータ(古典)
ハイパラ探索は既存のベイズ最適などを使って行うのでいいのかと思います。pytorchとoptunaみたいなので使いやすいと思います。もちろんblueqat+pytorchもOK。この辺りは既存の機械学習とそんなに大きくは変わらないと思います。
課題点(量子)
最近pytorchやtensorflowなどを量子に組み合わせるのが流行りそう(?)です。課題は、実機の量子コンピュータで行うと、上記の期待値導出に対して、サンプル数を十分に取る必要があります。
実際やってみると分かりますが、めちゃくちゃ計算量かかります。。。
MERA/TTN実装
量子回路を木構造に組みます。量子回路は可逆回路なので入出力の量子ビット数を揃える必要があります。回路途中にもつれを使いながら、組んでいきます。
入力には2種類の量子回路を準備しました。
出力ラベルには測定値の期待値の+1と-1を準備しました。学習率はe=0.01としました。


27.81962513923645秒でした。
次に、状態ベクトルを利用せず、サンプリングを使ってみました。(乱数シード固定するの忘れました)

収束しましたが、2147.1892235279083秒かかりました。。。100倍近くかかりました、、、やっぱり状態ベクトルからやるようにします。Tensorflow Quantumがシミュレータを選択したのも肯けます。
MPS

線一本書き忘れた、、、

14.297337532043457秒でした。MPSの方が軽いです。
最後にサンプリング精度
サンプリングの精度は結構大事なので、サンプルを減らしたら精度がどうなるか、簡単な回路でやってみます。
まず、状態ベクトルから、

7.313692092895508秒。早いです軽いMPSでやりました。シードも固定しました。
次、サンプリング。状態ベクトルの代わりに、サンプリング100回で。

38.05503296852112秒
サンプリング50回

22.827856063842773秒
サンプリング200回

68.8005166053772秒
悪くないですね。
150回

53.32575869560242秒
まぁ、こんなところでしょう。
MERA
今回作るモデルはMERAと呼ばれる木構造をしています。U3ゲートとCXゲートを使います。
|0> --[input]--U3--*--
|
|0> --[input]--U3--X--U3--*--
|
|0> --[input]--U3--*-- |
| |
|0> --[input]--U3--X--U3--X--[m]-[expt]-[loss]-[output]
#MERA circuit
def mera(a):
u = Circuit()
u.u3(a[0],a[1],a[2])[0]
u.u3(a[3],a[4],a[5])[1]
u.u3(a[6],a[7],a[8])[2]
u.u3(a[9],a[10],a[11])[3]
u.cx[0,1].cx[2,3]
u.u3(a[12],a[13],a[14])[1]
u.u3(a[15],a[16],a[17])[3]
u.cx[1,3]
return u
ツールを読み込み、初期設定をします。
from blueqat import Circuit
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import time
%matplotlib inline
np.random.seed(39)
#initial parameters
ainit = [np.random.rand()*np.pi*2 for i in range(18)]
必要な関数を実装します。
#expectation value
def E(sv):
return sum(np.abs(sv[:8])**2)-sum(np.abs(sv[8:])**2)
#loss function
def L(p,t):
return (p-t)**2
#data to gate
def ix(l):
u = Circuit(4)
for i in l:
u.x[i]
return u
データを準備します。トレーニング用のデータと検証用を準備しました。
#training data
inp = [[0,1],[2,3],[0],[3]]
tgt = [1,1,-1,-1]
#validation data
inp_c = [[1],[2],[0,2],[1,3]]
tgt_c = [-1,-1,1,1]
早速開始です。毎回の勾配の計算時に訓練データをランダムで選び最適化をかけます。
#initial parameters
a = ainit.copy()
#result list
ar = []
h = 0.01
e = 0.01
#iterations
nsteps = 800
start = time.time()
for i in range(nsteps):
r = np.random.randint(0,len(inp))
c = ix(inp[r])+mera(a)
loss = L(E(c.run()),tgt[r])
ar.append(loss)
at = [0 for i in range(len(a))]
for j in range(len(a)):
aa = a.copy()
aa[j] += h
loss2 = L(E((ix(inp[r])+mera(aa)).run()),tgt[r])
at[j] = a[j] - e*(loss2 - loss)/h
a = at
plt.plot(ar)
plt.show()
print(time.time() - start)
<Figure size 432x288 with 1 Axes>
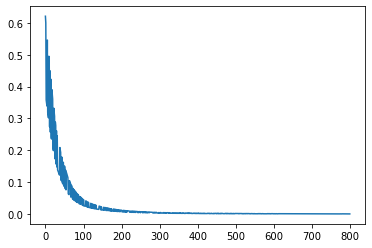
6.154975414276123
うまく収束したのでチェックしてみたいと思います。
#training accuracy
np.mean([E((ix(inp[i])+mera(a)).run())/tgt[i] for i in range(len(inp))])
#0.9760245973174358
0.9760245973174352
#validation accuracy
np.mean([E((ix(inp_c[i])+mera(a)).run())/tgt_c[i] for i in range(len(inp_c))])
#0.9769492668551134
0.953844587676994
いい感じですね。
MPS
次に作るのモデルはMPSと呼ばれる階段構造をしています。U3ゲートとCXゲートを使います。
|0> --[input]--U3--*--
|
|0> --[input]--U3--X--U3--*--
|
|0> --[input]---------U3--X--U3--*
|
|0> --[input]----------------U3--X--[m]-[expt]-[loss]-[output]
モデルは、
#MPS circuit
def mps(a):
u = Circuit()
u.u3(a[0],a[1],a[2])[0]
u.u3(a[3],a[4],a[5])[1]
u.u3(a[6],a[7],a[8])[2]
u.u3(a[9],a[10],a[11])[3]
u.cx[0,1]
u.u3(a[12],a[13],a[14])[1]
u.cx[1,2]
u.u3(a[15],a[16],a[17])[2]
u.cx[2,3]
return u
早速計算します。その他のパラメータ類は先ほどと同じにします。
start = time.time()
#initial parameters
a = ainit.copy()
#result list
ar = []
h = 0.01
e = 0.01
for i in range(nsteps):
r = np.random.randint(0,len(inp))
loss = L(E((ix(inp[r])+mps(a)).run()),tgt[r])
ar.append(loss)
at = [0 for i in range(len(a))]
for j in range(len(a)):
aa = a.copy()
aa[j] += h
loss2 = L(E((ix(inp[r])+mps(aa)).run()),tgt[r])
at[j] = a[j] - e*(loss2 - loss)/h
a = at
plt.plot(ar)
plt.show()
print(time.time() - start)
<Figure size 432x288 with 1 Axes>
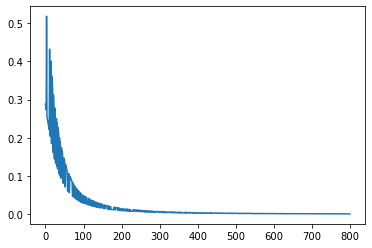
6.110741376876831
7.919758081436157
精度です。
#training accuracy
np.mean([E((ix(inp[i])+mps(a)).run())/tgt[i] for i in range(len(inp))])
#0.9697437828925157
0.9700788727843366
#validation accuracy
np.mean([E((ix(inp_c[i])+mps(a)).run())/tgt_c[i] for i in range(len(inp_c))])
#0.9696755262709482
0.970138094683916
まとめ
既存の機械学習の叡智を取り込むことで進捗があります。ポイントは、
1、モデルはこれから世界中で提案される。うちはテンソルネット使う。
2、測定と期待値あたりがちょっとコツが必要。
3、期待値の導出などは意見ありそうだけど、pytorch使いたいです。
4、一応VQEみたいな変分計算知ってるとデバッグに便利は便利
かなり計算量が必要。実機でやるにはさらにサンプリングという壁があるので、辛みはありますが、色々アイデアあるので頑張りましょう。
今後はよりデータ量と量子ビット数を増やしたいと思います。今回は4量子ビットでしたが、世界中で量子機械学習がこれくらいの量子ビット数に落ち着いている理由がなんとなく分かりました。
以上です。
