興奮しますね。誰ですか量子ゲートの実用化は遠いといった人は。今回は289量子ビットを利用したQAOAと呼ばれる量子ゲート向けのアルゴリズム論文をさっそく解説します!
レビューする論文
Quantum Optimization of Maximum Independent Set using Rydberg Atom Arrays
S. Ebadi1,∗ , A. Keesling1,2,∗ , M. Cain1,∗ , T. T. Wang1 , H. Levine1,‡ , D. Bluvstein1 , G. Semeghini1 , A. Omran1,2 , J.-G. Liu1,2 , R. Samajdar1 , X.-Z. Luo2,3,4 , B. Nash5 , X. Gao1 , B. Barak5 , E. Farhi6,7 , S. Sachdev1,8 , N. Gemelke2 , L. Zhou1,9 , S. Choi7 , H. Pichler10,11, S.-T. Wang2 , M. Greiner1,† , V. Vuletic´ 12,† , M. D. Lukin1,†
1Department of Physics, Harvard University, Cambridge, MA 02138, USA 2 QuEra Computing Inc., Boston, MA 02135, USA 3Department of Physics and Astronomy, University of Waterloo, Waterloo N2L 3G1, Canada 4Perimeter Institute for Theoretical Physics, Waterloo, Ontario N2L 2Y5, Canada 5 School of Engineering and Applied Science, Harvard University, Cambridge, MA 02138, USA 6Google Quantum AI, Venice, CA 90291 7Center for Theoretical Physics, Massachusetts Institute of Technology,Cambridge, MA 02139 8 School of Natural Sciences, Institute for Advanced Study, Princeton, NJ 08540, USA 9Walter Burke Institute for Theoretical Physics, California Institute of Technology, Pasadena, CA 91125 10Institute for Theoretical Physics, University of Innsbruck, Innsbruck A-6020, Austria 11Institute for Quantum Optics and Quantum Information, Austrian Academy of Sciences, Innsbruck A-6020, Austria 12Department of Physics and Research Laboratory of Electronics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA ∗ These authors contributed equally to this work ‡ Current affiliation: AWS Center for Quantum Computing, Pasadena, CA 91125 † Corresponding authors
布陣がやばすぎですね。同じ業界で仕事してるとは思えないレベルです。
マシン
今回利用されるのはハーバード大学やMITで開発された冷却原子と呼ばれる、原子を光ピンセットで捕獲し、それを絶対零度近くまで冷やして計算する冷却原子マシンです。
組合せ最適化問題
問題は組合せ最適化問題と呼ばれるものです。多くの選択肢の中から最も良いものを選びます。
問題設定
グラフの形に問題を設定し、頂点と辺に重みをつけて定式化のエネルギーが一番小さくなるようにときます。今回はMIS(Maximal Independent Set)と呼ばれる、隣接する頂点が存在しない頂点の集合のうち、頂点数が最大の最大独立集合(https://37zigen.com/maximum-independent-set-algorithm/)という問題を解きます。
概要
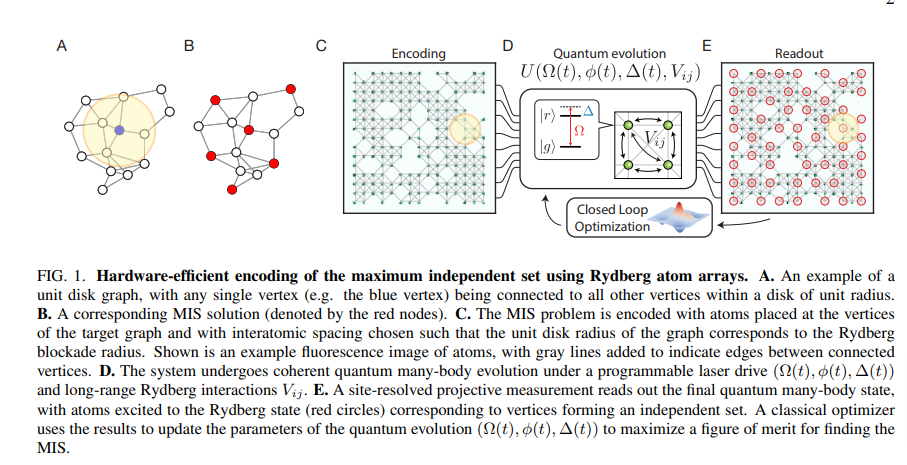
引用:https://arxiv.org/pdf/2202.09372.pdf
組合せ最適化問題をグラフ問題として実装し、今回はリュードベリブロケード半径を利用して解きます。今回利用する原子は一般的にリュードベリ原子と呼ばれ、電子の励起状態にリュードベリ状態と呼ばれる原子核から遠い位置での励起を利用することにより、電子同士が干渉し、一定の半径内では2つの原子が同時にリュードベリ状態にいることができないという特性を利用しています。
グラフ問題はこのリュードベリブロッケードと相性のいいMISが採用されています。空間位相変調器で原子を捕獲したら、動的光ピンセットで所望のグラフ問題へ原子を移動させ、量子時間発展計算をリュードベリレーザーを利用して解きます。その読み出し結果をさらに最適化するようにパラメータ類を変更しながらQAOAをかけます。
QAOAは量子断熱時間発展の理論の元に、ハミルトニアンを断熱過程で変化させ、最終的に求めたいハミルトニアンの基底状態を探索するものです。今回はパラメータはリュードベリマシンを利用した専用のハミルトニアンに対して、リュードベリレーザーにおいていくつかの時間のパラメータがあり、それを利用してQAOAをかけているようです。相互作用の項にはまさにリュードベリ半径が利用されています。
今回はQAOAとVQAAという二種類のアルゴリズムで実装をして速度を図り、SAとも比較をしています。かなり特殊な計算かつパラメータで冷却原子特有の技術と知識が必要ですので、一般の量子回路への展開はかなり難しいという印象を受けました。
ただ、N=80やN=289のような今までの量子マシンでは到達できない量子ビット数の量子シミュレーションを行っているうえ、その評価もテンソルネットワークなどの最新のシミュレーションテクニックが必要です。
まとめ
今回はリュードベリ原子を利用した冷却原子マシンで、特に有利な組合せ最適化問題を解いたという論文でした。専門性が高く汎用はかなり低めでした。まだ続報や続きの研究を見ていかないと一般企業の活用は難しいと感じました。以上です。
