最近いくつかテンソルネットワークに入門してみたいけど仕組みがわからないということもあるようなので、解説をします。テンソルネットワークは大変注目されている技術です(多分)。
テンソルネットワークにまつわる質問で誤解が多いのが、
「テンソルネットワークは近似しているので精度が低い」
というものです。テンソルネットワークを使う限りでは、SVDを使わなければ特に精度は下がりません。計算の順序を工夫するだけでも早くなることがありますので、近似を使うというのは必ずしもテンソルネットワーク全般に当てはまることではありません。ですので、少しずつ機会を見てこうしたテンソルネットワークの技術を紹介していきます。
まず、量子コンピュータのシミュレーションにおけるテンソルネットワークを見てみます。テンソルとはベクトルや行列などの総称を言いますが、量子コンピューティングの文脈で、特に状態ベクトルシミュレータと呼ばれる従来型のシミュレータの文脈では、スカラー量、ベクトル、行列を覚えておけば十分かと思います。

ベクトルは量子状態を記述する状態ベクトルに。行列は量子状態を変化させる量子ゲートに対応しています。スカラー量は確率振幅や期待値などに対応しますが、状態ベクトルシミュレーションをする際には一般的には状態ベクトルからそれらの量を求めますので、最悪ベクトルと行列だけ知っていれば大丈夫な気もします。
量子コンピュータ関連の計算でテンソルネットワークが登場する際には、縮約と特異値分解が主になります。ただ、状態ベクトル計算で後者が出るのは稀なので、縮約(しゅくやく)だけ覚えれば良いかと思います。縮約は異なるテンソル同士の計算をしますが、繋がっている腕を介して計算をします。腕が繋がっていないところは計算ができません(基本的には)。よく質問でテンソルネットワークには近似が入るので精度が下がるというのは、この右側の特異値分解(SVD)を実行したあと、かつ下図の真ん中の対角行列をカットオフした場合になります。今回は縮約のみを使いますので、あまり関係はありません。

量子コンピュータの回路をシミュレーションする際には、左に量子ビット、右に量子ゲートを量子回路上に起きます。ちょっと記述が厳密には微妙なところもありますが、このままやってみます。状態ベクトルとは、量子ビットの状態を0と1のでる確率に対応する確率振幅が格納されたベクトルです。

量子回路のシミュレーションについてテンソルネットワークと状態ベクトルの関係についてみてみます。テンソルネットワークでは、状態ベクトルはかく量子ビット同士独立して持つことができますが、状態ベクトルシミュレーションでは、大きな状態ベクトルに統合する必要があります。よく教科書では、量子ビットの状態ベクトル同士のテンソル積を取ることによって大きな状態ベクトルを作ることができます。
下の図では、[1,0]の量子状態を持つ初期化された2つの|0>状態の量子ビットが、右側ではテンソル積を取ると一つの大きな状態ベクトルになっています。[1,0,0,0]というように、2^2の要素サイズになりました。

次に、量子ゲート計算ですが、状態ベクトルを一つにまとめる際には、量子ゲート自体も補完が必要です。上の量子ビットにXゲートをかける際には、下の量子ビットには特に量子ゲートは設定されていませんが、そこに単位行列Iを補完して、量子ゲート同士のテンソル積を取ることで、先ほどの状態ベクトルに作用をさせることができます。結果として、4*4の行列ができます。

次に記述が微妙と言っていた部分です。2量子ビットゲートは4*4行列なのですが、図ではテンソルっぽく書いてしまっています。テンソルネットワークと量子回路の標準的な記述はルールが異なるのでちょっと混乱します。下記の左側は正確にはorder-4のテンソルなのですが、reshapeすることで、腕2本の行列に変更ができます(ていうか元から行列ですが)。
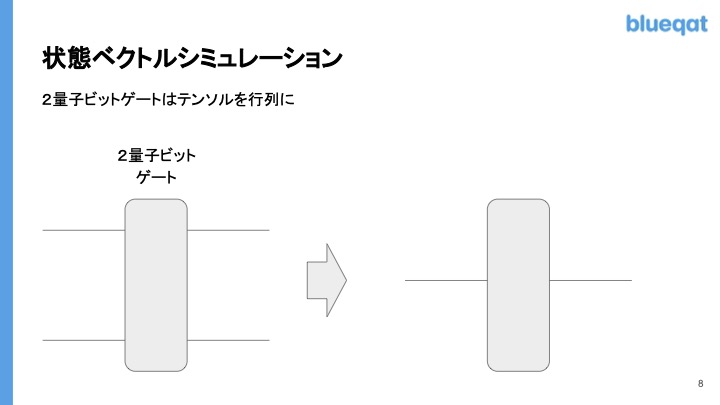
ということで、これらを全て統合すると、一見複雑に見える量子回路は、元の状態ベクトルに対して、各時間における量子ゲートの縦のテンソル積をとった大きな行列を順に計算するという形になり、テンソルネットワークで表現すると右側のような串団子になります。

そして、腕が繋がっている部分を縮約すると計算に相当し、最終的には腕が一本の状態ベクトルとなります。

テンソルネットワーク自体はできることが大変多く、今回は状態ベクトルシミュレーションの実行をテンソルネットワークで表現してみました。教科書やリファレンスがない分野ですが、一つずつ見ていくとわかりやすいかと思います。以上です。
