Accelerating QAOA with CUDA-Q and H100 GPU: Solving the MaxCut Problem via Quantum Simulation

We conducted a simulation of the MaxCut problem using one of the most prominent quantum algorithms—QAOA (Quantum Approximate Optimization Algorithm). In this study, we used CUDA-Q to compare the execution speed and optimization accuracy between CPU and GPU environments.

All experiments were performed with the same random seed and identical problem setup (graph structure) for fair comparison.

🎯 What is the MaxCut Problem?

The MaxCut problem involves dividing the nodes of a graph into two sets such that the number (or total weight) of edges between the sets is maximized. QAOA is a quantum algorithm designed to approximately solve such combinatorial optimization problems using quantum circuits.

🧪 Experimental Setup

• CUDA-Q framework used
• QAOA depth: 2 layers
• Optimizer: Nelder-Mead
• Fixed random seed (for reproducibility)
• Same Erdős–Rényi random graph used across all runs
• CPU: Google Colab (standard CPU)
• GPU: NVIDIA H100 80GB

⚙️ Execution Results

Example of the problem graph:

Example of optimization steps:

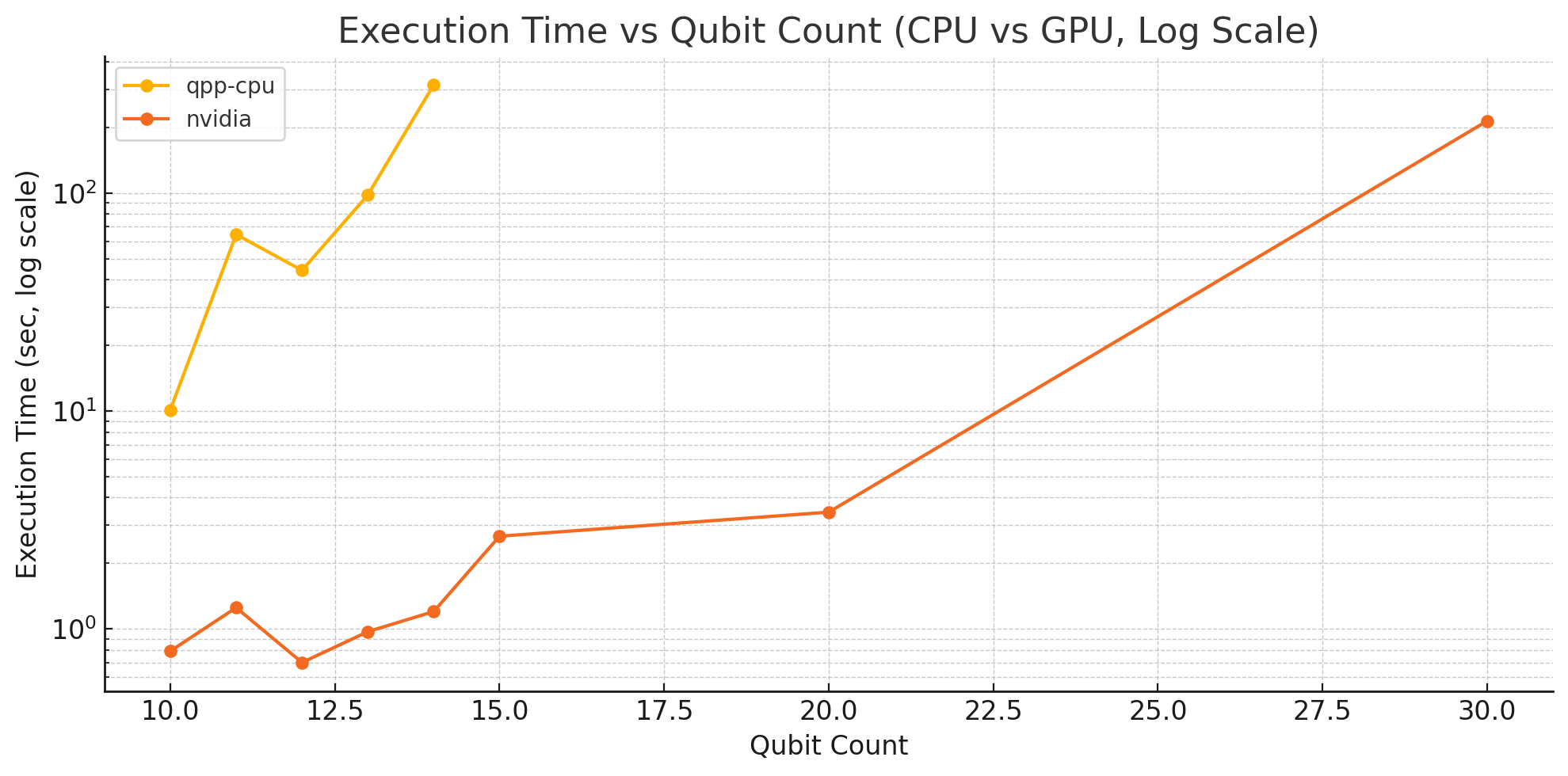
Comparison of qubit count vs. execution time shows that as the number of qubits increases, the resulting MaxCut value tends to increase as well.

However, since QAOA is a combinatorial optimization method, the execution time heavily depends on how quickly the optimizer converges, which can vary significantly. This makes it difficult to obtain a smooth or consistent execution time graph.

🔍 Discussion

• Even for the same problem, the GPU completed optimization much faster than the CPU.
• The GPU was able to handle 15 to 20 qubits very quickly, but for 30 qubits, execution time exceeded 200 seconds due to increased circuit complexity.
• Optimization performed directly on the GPU greatly accelerated the overall process.

🚀 Conclusion

GPU-based quantum simulation has proven to be highly effective for mid-scale algorithms like QAOA. Going forward, we plan to further evaluate GPU performance with larger-scale circuits and other quantum algorithms.