こんにちは、tensorflow quantumでは、量子強化学習におけるデータ入力を行っています。使われている量子回路はXanaduの論文が基本となっています。
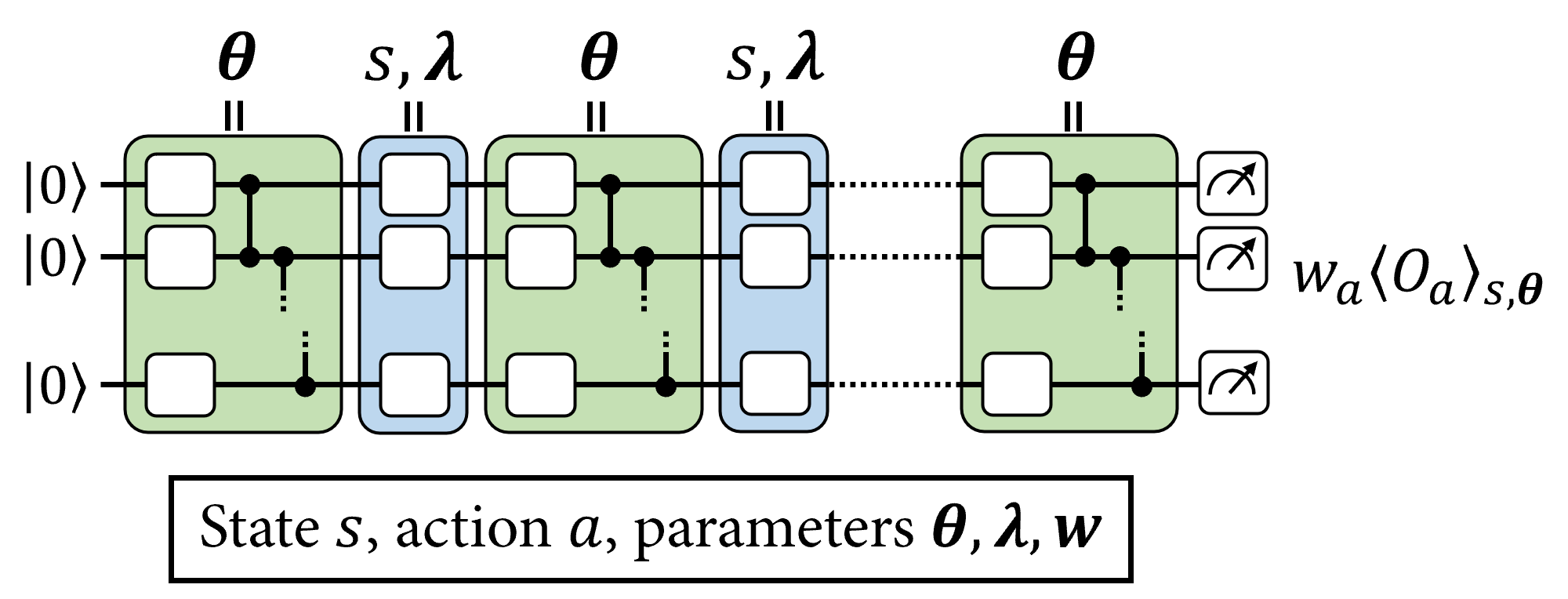
引用:https://www.tensorflow.org/quantum/tutorials/quantum_reinforcement_learning?hl=ja
肝はこの構成となっていて、Θの部分とs/λの部分と別れています。Θの部分が変分回路と呼ばれる角度を入れて量子回路を学習させる部分で、sの部分がデータ入力となっています。これらの構成はxanaduの回路がベースとなっていて、最終的に状態を入力した量子機械学習では、policy-gradient型とDeep-Q-Learning型共に同じ回路を使っています。
参考:
The effect of data encoding on the expressive power of variational quantum machine learning models
Maria Schuld, Ryan Sweke, Johannes Jakob Meyer
https://arxiv.org/pdf/2008.08605.pdf
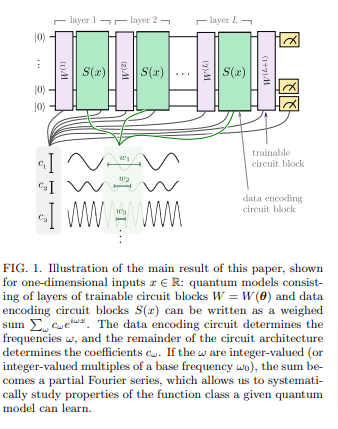
引用:https://arxiv.org/pdf/2008.08605.pdf
仕組みはわかりやすくて、量子コンピュータの量子ゲートは回転によって関数を表現し、1つのブロックだけでは、サイン関数しか表現できないのですが、複数重ねることで、フーリエ級数を表現でき、複雑な関数を表現できるというものです。
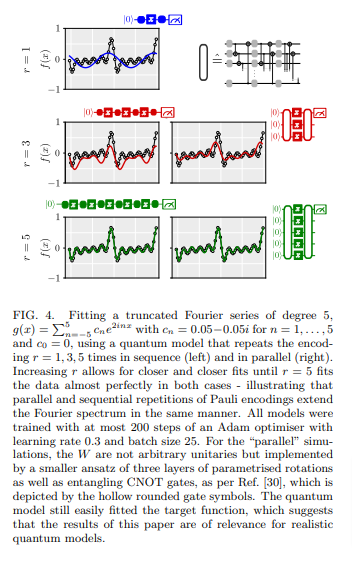
引用:https://arxiv.org/pdf/2008.08605.pdf
実際には複数量子ビットをもつれさせるか、もしくは深さ方向に重ねるという方法があります。2量子ビットゲートはコストが高いので、繰り返し計算してフーリエ級数を構成するほうがよさそうです。
wikipediaはこちらです。
フーリエ級数
https://ja.wikipedia.org/wiki/%E3%83%95%E3%83%BC%E3%83%AA%E3%82%A8%E7%B4%9A%E6%95%B0
量子回転ゲートは複素数ですので、複素フーリエ級数というのをつかい、
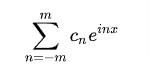
こちらを作ることになります。これは時間発展演算子の形ですので、ハミルトニアンの時間発展の係数として実現することができます。
量子機械学習を学習するのにハミルトニアンの時間発展のようなシミュレーションの技術も出てきますが、とても分かりやすい内容かと思いました。以上です。
