どうも、量子業界でやる気のないランキング下から3番目のミナトです。中国の暗号解読が話題です。
[FT]中国研究者、量子コンピューターで「暗号解読」主張
https://www.nikkei.com/article/DGXZQOCB05B5N0V00C23A1000000/
これから少しずつ勉強会とブログ記事で中身を明らかにしていきますが、今回は単純に論文中のコスト関数を手元のQAOAで計算してみたいと思います。
大分前に作ったサイトがあるので、こちらを使ってみます。機能が足りないので、後半はjupyterを使って確認をしてみます。
論文はこちらです。
Factoring integers with sublinear resources on a superconducting quantum processor
https://arxiv.org/abs/2212.12372
appendixにコスト関数がありましたので、ひとずつどんなもんか計算してみます。
論文中は量子ビットの通し番号が1からになっていますが、計算の都合上0からに変更をします。
また、単位行列は最小値問題に影響しないので、定式化に入れますが、量子回路計算からは外して問題ないので外します。
3量子ビットで1961を素因数分解したコスト関数はp.16に書いてありますね。
Hc3 = 43.5*I-4*Z(0)*Z(1)+2.5*Z(0)*Z(2)-1.5*Z(0)+3*Z(1)*Z(2)-3.5*Z(1)-4*Z(2)
となっています。ここから、43.5*Iを外して、
Hc3' = -4*Z(0)*Z(1)+2.5*Z(0)*Z(2)-1.5*Z(0)+3*Z(1)*Z(2)-3.5*Z(1)-4*Z(2)
で計算してみます。あとでjupyterで計算しますが、以前便利なものを作ったので、こちらを使います。
ノーコードでQAOAができます。

実際に入れて計算してみます。
ちなみに3量子ビットありますので、答えに到達するのはランダムに計算して、1/8=0.125となりますので、12.5%です。
何回か計算してみました。論文から答えは001とわかっていますが、やはり初期状態などから間違えることも多々ありました。
論文では、p=3がよかったとありますが、まずはp=1からやってみます。30%程度は答えが出るのでいい感じです。

ちなみに量子回路も出力されますが、p=1の回路はこんな感じです。
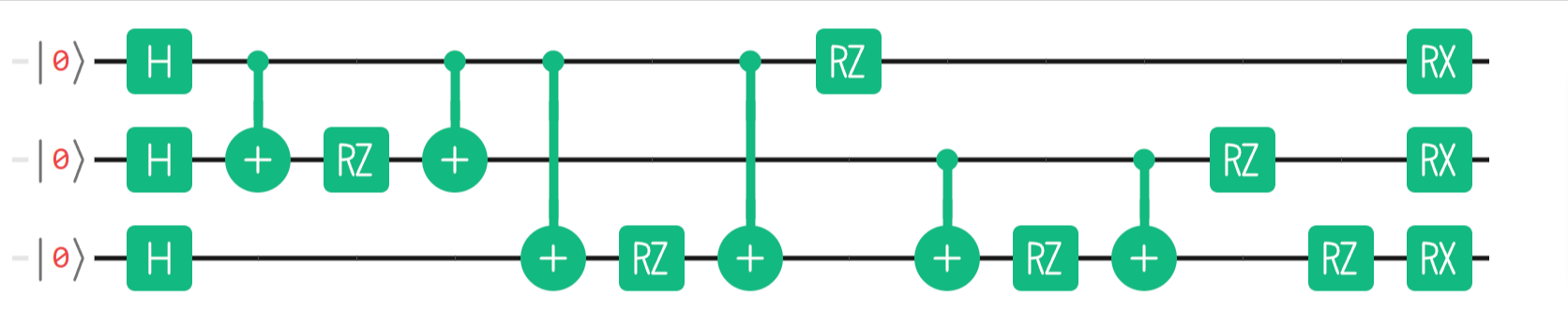
次にp=3もやってみます。なんと、ぐっと正解率が上がりました!p=3は論文通り、かなりよさそうですね!

量子回路p=3では3倍の長さになります。最適化するパラメータ数は3*2=6となります。

ちなみに、論文中での正解のコスト関数が提示されていて、
001が33
100が35
000が36
100が42
ですので、上記のコスト関数に値を代入しますが、元のハミルトニアンのZの期待値は0の時には+1、1の時には-1をいれますので、元式への代入は、
C(Hc3) = 43.5-4*1*1+2.5*1*(-1)-1.5*1+3*1*(-1)-3.5*1-4*(-1) = 33
となり、確認することができます。
次に5量子ビットで48567227の素因数分解ですが、いろいろやってみたのですが、コスト関数と値が合わなかったので、最初からより詳しく検証する必要が出たため、いったん検証を中止しました(時間がかかりそう)。
3量子ビットの場合だけになってしまいましたが、コスト関数があってれば答えはとりあえず出ることはわかりました。今回は全結合の検討などあまり3量子ビットでもできなかったので、より論文のいろいろなテクニックを今後ブログでも見ていきたいと思います。
