量子ニューロンの量子計算における実装について

はじめに

量子コンピュータは最近ではNISQと呼ばれる近年のエラーありのタイプを既存計算機とのハイブリッドで利用し、各種の問題を解くために利用するというのが流行っています。

NISQは基本的にはあまり速度がでず、ハイブリッドが足かせになりますが行列の固有値の期待値を求められたりと一定の計算をすることができるため、この辺りの計算を利用したアルゴリズムやアプリケーションが提案されています。

一方で、純粋量子計算を利用した新しい計算手法やモデルの構築に対しても引き続き提案が続いています。今回は後者の方法でニューロン計算を再現するためのものを確認したいと思います。

論文

Quantum Neuron: an elementary building block for machine learning
on quantum computers
Yudong Cao,1, ∗ Gian Giacomo Guerreschi,2, † and Alán Aspuru-Guzik1, 3, ‡
1Department of Chemistry and Chemical Biology,
Harvard University, Cambridge, MA 02138
2Parallel Computing Lab, Intel Corporation, Santa Clara, CA 95054
3Senior Fellow, Canadian Institute for Advanced Research, Toronto, Ontario M5G 1Z8, Canada

https://arxiv.org/pdf/1711.11240.pdf

今回はこちらをみていきます。

参考

唯一無二の参考文献

「量子コンピュータでニューラルネットワークな論文紹介　〜量子ニューロンの実装〜」

数式に関してこちらの参考は文句がないので、こちらを参考にしたいと思います。

既存計算機と量子計算機のニューロンの比較

ニューラルネットワークの多層パーセプトロンと呼ばれるモデルの構築のために、単体のノードの和に活性化関数という関数を適用してある値を取り出すプロセスを量子回路を使って行うのが今回の目的です。

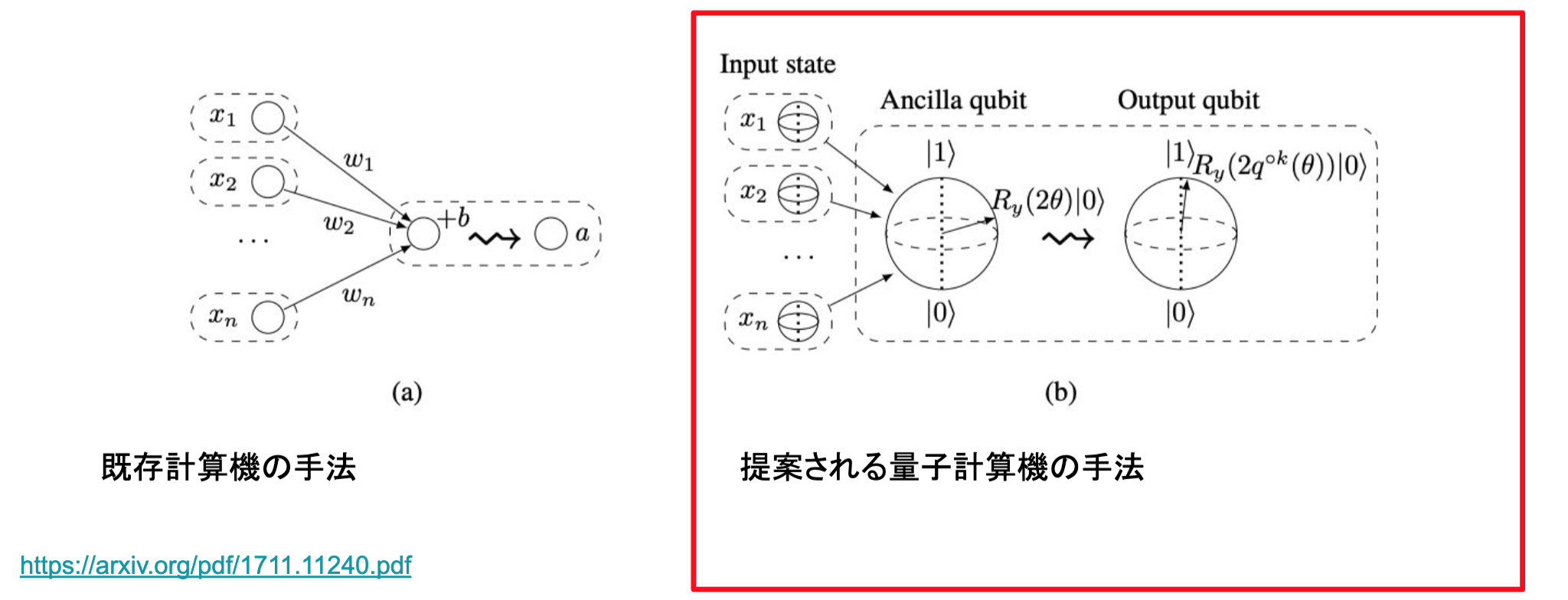
既存手法のおさらい

ノードの値xに結合荷重wをかけて足し合わせ、それにバイアスを付加して、活性化関数と呼ばれる関数を適用します。

活性化関数には通常非線形なものを使います。
##なぜ非線形なものを使うのか
こちらに書いてありました。

「活性化関数のまとめ（ステップ、シグモイド、ReLU、ソフトマックス、恒等関数）」

なぜ多層パーセプトロンで線形関数を使わないのか？理由は、活性化関数に線形関数を用いるとニューラルネットワークで層を深くすることの意味がなくなるからです。線形関数の問題点は、どんなに層を深くしても、それと同じことを行う「隠れ層のないネットワーク」が必ず存在する、という事実に起因します。簡単な例として、線形関数h(x)=cxを活性化関数として３層重ねるとy=h(h(h(x))になります。つまりこれは、y=ccc*x(y=ax)というように隠れ層のないネットワークでも表現できてしまいます。この例のように、活性化関数に線形関数を用いると多層にすることの利点を生かすことができません。つまり、それは無駄に処理を増やすことにつながるかもしれないので、活性化関数に線形関数を用いるべきではありません。

引用ですが、線形関数にしてしまうとディープに意味がなくなってしまいます。非線形な関数を使います。

量子ゲート計算は線形計算

量子ゲート計算は基本的にはパウリ演算を基本としており、行列の線形計算となります。それらの行列計算をうまく使って、上記の非線形な関数を作るのが今回の目的です。

X = [0  1
     1  0]

Y = [0 -i
     i  0]

この辺りをうまく使っていきます。

手順

手順はシンプルです。

１、入力回路
２、加算回路
３、活性化関数回路

この三ステップです。早速みていきます。

１、入力回路

データの入力はXゲートを使います。これを使うと0の値を1に、1の値を0にできます。量子ビットと呼ばれる回路を入力値の数だけ用意します。基本は0に初期化されますので、Xゲートで所望の回路を1にします。

２、加算回路

加算回路はRyゲートというのを使い、回転を使って表現します。さらにRyゲートでも制御Ryゲートと呼ばれる、コントロールビットが1の時だけRyゲートを適用するというゲートを利用することで、xの値が1の時だけ回転を適用するというものを使います。

回転させる量子ビットはアンシラビットと呼ばれる今回の回転のために用意された余剰ビットです。

こうすることによって、アンシラに角度が足されていきます。そして、バイアスの角度を足すと所望の加算された値が得られます。結合荷重の値はそれぞれのControlled-Ryゲートの角度の部分に設定しておきます。

３、活性化関数回路

そして最後の活性化関数回路です。こちらは下記の赤枠部分で実現できるようです。

ほとんどは参考先の資料に計算がありますので、そちらの参考＆補足でやります。いくつかコツがあります。まずは、
Controlled-YゲートとRz(-pi/2)は組み合わせて省略できます。こちらはテンソル積で表現することができます。

CY = [1 0 0  0
      0 1 0  0
      0 0 0 -i
      0 0 i  0]

Rz(-pi/2) = [1 0           = [1 0            = [1  0
             0 e^i(-pi/2)]    0 isin(-pi/2)]    0 -i]

CY*Rz(-pi/2)⊗I = [1         = [1
                    1            1
                      0 -1         0    -i*(-i)
                      1  0]        -i*i       0]

こうなりました。アンシラに加算がうつったとして、上記のアンシラとアウトプットの量子ビットの計算は、参考文献より、

\mid 0 \rangle \otimes \mid\psi\rangle

まずはこちらを準備します。まず加算をすると、

(cos\theta I -i sin\theta Y)\mid 0 \rangle \otimes \mid \psi \rangle

ここで、

-iY = X

より、

(cos\theta \mid 0 \rangle + sin\theta X \mid 0 \rangle) \otimes \mid \psi \rangle\\ = (cos\theta \mid 0 \rangle + sin\theta \mid 1 \rangle) \otimes \mid \psi \rangle\\

次に制御ゲートControlled-(-iY)を適用して、こちらも参考文献のままですが、|1>の方にだけゲートがかかります。

cos\theta \mid 0 \rangle \otimes \mid \psi \rangle - i sin\theta \mid 1 \rangle \otimes Y \mid \psi \rangle

そして、Ry(2θ)の転置をかけると、

(cos\theta I +isin\theta Y) * cos\theta \mid 0 \rangle \otimes \mid \psi \rangle +(cos\theta I +isin\theta Y) * (- i sin\theta \mid 1 \rangle) \otimes Y \mid \psi \rangle

ここで展開すると、-iY = XよりうまくX|0> = |1>と、X|1> = |0>が現れ、まとめると、

の参考の通り、

A\mid 0 \rangle \otimes R_y(2arctan(tan^2\theta))\mid \psi \rangle - B\mid 1 \rangle \otimes R_y(-\pi /2)\mid \psi \rangle

の形になります。これは、アンシラが0の時に非線形の活性化関数が適用され、アンシラが1の時には関係ない回転が適用されます。

4.そこでRUS回路

Repeat Until Success回路によって、アンシラの測定が0の時にしか成り立たないですが、成功するまで初期化して答えを取り出すということをします。

ということでBlueqat実装

理論だけではという話になりますので、python実装してみます。

例として、1011の４量子ビットの回路の入力に対して、角度が0.1,0.2,0.3,0.4の結合荷重の回路、バイアスが0.2、arctan(tan^2)の回路を作ってみます。

まず加算回路です。加算回路はCRyゲートで実現できるのでした。
今回のBlueqatはまだCRyが実装されいないため、代わりにCU3を使います。
U3は、

U3(\theta, \phi, \lambda) = \begin{pmatrix} \cos\left(\frac{\theta}{2}\right) & -e^{i\lambda} \sin\left(\frac{\theta}{2}\right) \\ e^{i\phi} \sin\left(\frac{\theta}{2}\right) & e^{i(\lambda + \phi)} \cos\left(\frac{\theta}{2}\right) \end{pmatrix}

となり、Ryは

U3(\theta, 0, 0)

で実現できます。CU3はそのU3の制御ゲート付きなので、

CU3(\theta, 0, 0)

でRyができます。試しにRyとU3を比較してみると、

from blueqat import Circuit
Circuit().ry(0.1)[0].run()

array([0.99875026+0.j, 0.04997917+0.j])

Circuit().u3(0.1, 0, 0)[0].run()

array([0.99875026+0.j, 0.04997917+0.j])

と、全く同じになりました。制御ゲートをつけてみると、

Circuit().cu3(0.1, 0, 0)[0,1].run()

array([1.+0.j, 0.+0.j, 0.+0.j, 0.+0.j])

Circuit().x[0].cu3(0.1, 0, 0)[0,1].run()

array([0.        +0.j, 0.99875026+0.j, 0.        +0.j, 0.04997917+0.j])

q[0]==0の時は無反応、q[0]==1の時は、10と11の状態ベクトルがきちんとU3と揃ってます。

例として、1011の４量子ビットの回路の入力に対して、角度が0.1,0.2,0.3,0.4の結合荷重の回路、バイアスが0.2、arctan(tan^2)の回路を作ってみるでしたので、まずはXゲートで入力値の1011を表現し、その後CU3を連続してかけることで、加算をします。最後にバイアスを足すところまでやってみますと、アンシラを含めて５量子ビット用意し、

Circuit(5).x[0,2,3].cu3(0.1*2,0,0)[0,4].cu3(0.2*2,0,0)[1,4].cu3(0.3*2,0,0)[2,4].cu3(0.4*2,0,0)[3,4].u3(0.2*2,0,0)[4].run()

array([0.        +0.j, 0.        +0.j, 0.        +0.j, 0.        +0.j,
       0.        +0.j, 0.        +0.j, 0.        +0.j, 0.        +0.j,
       0.        +0.j, 0.        +0.j, 0.        +0.j, 0.        +0.j,
       0.        +0.j, 0.54030231+0.j, 0.        +0.j, 0.        +0.j,
       0.        +0.j, 0.        +0.j, 0.        +0.j, 0.        +0.j,
       0.        +0.j, 0.        +0.j, 0.        +0.j, 0.        +0.j,
       0.        +0.j, 0.        +0.j, 0.        +0.j, 0.        +0.j,
       0.        +0.j, 0.84147098+0.j, 0.        +0.j, 0.        +0.j])

bin(13) = 01101とbin(29) = 11101に相当する量子ビットが状態ベクトルとして出てきます。アンシラビットがある角度を持っていることがわかります。これは、

1*0.1+0*0.2+1*0.3+1*0.4+0.2 = 1

のRy回転の角度に相当し、

Circuit().u3(1*2,0,0)[0].run()

array([0.54030231+0.j, 0.84147098+0.j])

のように簡単に確認ができます。状態ベクトルは[0.54030231, 0.84147098]より、
実機の場合には、

|0>は0.540302310.54030231 = 0.29192658619133605
|1>は0.841470980.84147098 = 0.7080734101821604

のそれぞれの確率で出ることになり、

Circuit(5).x[0,2,3].cu3(0.1*2,0,0)[0,4].cu3(0.2*2,0,0)[1,4].cu3(0.3*2,0,0)[2,4].cu3(0.4*2,0,0)[3,4].u3(0.2*2,0,0)[4].m[:].run(shots=1000)

Counter({'10111': 716, '10110': 284})

こうすることでだいたい良さそうな感じで出てきます。実機の場合にはこういう風に確認をします。

活性化関数実装

大事なのはこれからで、活性化関数を実装します。inputに4量子ビット、ancillaに1量子ビット、outputに1量子ビット必要ですので、６量子ビットでやってみます。まずは入力からアンシラに加算をし、アウトプットに制御ゲートをかけて、Rz回転して、最後Ryのエルミート転置をとります。

import math

A = Circuit(5).x[0,2,3].cu3(0.1*2,0,0)[0,4].cu3(0.2*2,0,0)[1,4].cu3(0.3*2,0,0)[2,4].cu3(0.4*2,0,0)[3,4].u3(0.2*2,0,0)[4]
B = Circuit(5).cu3(math.pi,0,0)[4,5].rz(-math.pi/2)[4]
C = Circuit(5).cu3(0.1*2,math.pi,math.pi)[0,4].cu3(0.2*2,math.pi,math.pi)[1,4].cu3(0.3*2,math.pi,math.pi)[2,4].cu3(0.4*2,math.pi,math.pi)[3,4].u3(0.2*2,math.pi,math.pi)[4]

(A+B+C).run()

array([ 0.        -0.j        ,  0.        -0.j        ,
        0.        -0.j        ,  0.        -0.j        ,
        0.        -0.j        ,  0.        -0.j        ,
        0.        -0.j        ,  0.        -0.j        ,
        0.        -0.j        ,  0.        -0.j        ,
        0.        -0.j        ,  0.        -0.j        ,
        0.        -0.j        ,  0.20642327+0.20642327j,
        0.        -0.j        ,  0.        -0.j        ,
        0.        +0.j        ,  0.        +0.j        ,
        0.        +0.j        ,  0.        +0.j        ,
        0.        +0.j        ,  0.        +0.j        ,
        0.        +0.j        ,  0.        +0.j        ,
        0.        +0.j        ,  0.        +0.j        ,
        0.        +0.j        ,  0.        +0.j        ,
        0.        +0.j        , -0.32148519-0.32148519j,
        0.        +0.j        ,  0.        +0.j        ,
        0.        -0.j        ,  0.        -0.j        ,
        0.        -0.j        ,  0.        -0.j        ,
        0.        -0.j        ,  0.        -0.j        ,
        0.        -0.j        ,  0.        -0.j        ,
        0.        -0.j        ,  0.        -0.j        ,
        0.        -0.j        ,  0.        -0.j        ,
        0.        -0.j        ,  0.50068352-0.50068352j,
        0.        -0.j        ,  0.        -0.j        ,
        0.        +0.j        ,  0.        +0.j        ,
        0.        +0.j        ,  0.        +0.j        ,
        0.        +0.j        ,  0.        +0.j        ,
        0.        +0.j        ,  0.        +0.j        ,
        0.        +0.j        ,  0.        +0.j        ,
        0.        +0.j        ,  0.        +0.j        ,
        0.        +0.j        ,  0.32148519-0.32148519j,
        0.        +0.j        ,  0.        +0.j        ])

となりまして、bin(13),bin(29),bin(45),bin(61)に相当します。

で、アンシラが0の時のものを採用するのでした。その時の出現確率は、

a = abs(0.20642327+0.20642327j)**2
a

0.08522113279498578

b = abs(0.50068352-0.50068352j)**2
b

0.5013679743991809

となりました。期待値は、

b/(a+b)

0.854717498586661

となりました。確認をするには、、、単純にRy(2*arctan(tan(θ)**2))を計算して期待値を出してみます。

result = Circuit().ry(2*math.atan(math.tan(1)**2))[0].run()
result

array([0.38115941+0.j, 0.92450933+0.j])

a = abs(result[0])**2
b = abs(result[1])**2

b/(a+b)

0.8547175017806217

ほぼ同じになりました。念の為他の角度でも調べてみましたが大丈夫そうです。

ということで！

非線形の活性化関数を量子計算で実装する論文をpythonで再現できました（たぶん）！

ちなみに今回のは推論ですが、学習が問題になるのでは？ということですがその通りのようです。
評価関数なしの最適化計算などで実現できるかも？ということでした。誤差逆伝搬法の代わりに最適化を使うのは、

「誤差逆伝播法 vs vcopt、ニューラルネットの学習アルゴリズム比較」
https://vigne-cla.com/9-10/

この辺りをご参考に！