今回は具体的な問題を解く回です。
参考はこちら。
https://queracomputing.github.io/Bloqade.jl/dev/tutorials/5.MIS/main/
最大独立集合問題を二種類の解き方で行っています。結論から言うとアナログ量子シミュレーションのほうが成績が良いです。では見てみましょう。
最大独立集合問題MIS
MIS(Maximal Independent Set)と呼ばれる、隣接する頂点が存在しない頂点の集合のうち、頂点数が 最大の最大独立集合。 見た感じリュードベリ量子シミュレータと相性よさそうです。
問題グラフ作成
最初はグラフを作ります。
using Graphs
using Bloqade
using Random
using GenericTensorNetworks
using Optim
using PythonCall
plt = pyimport("matplotlib.pyplot");
グラフは4*4で、距離は4.5マイクロメートル離れています。16個原子を作りますが、そのうち0.2の割合で落とします。
Random.seed!(2)
atoms = generate_sites(SquareLattice(), 4, 4; scale = 4.5) |> random_dropout(0.2)
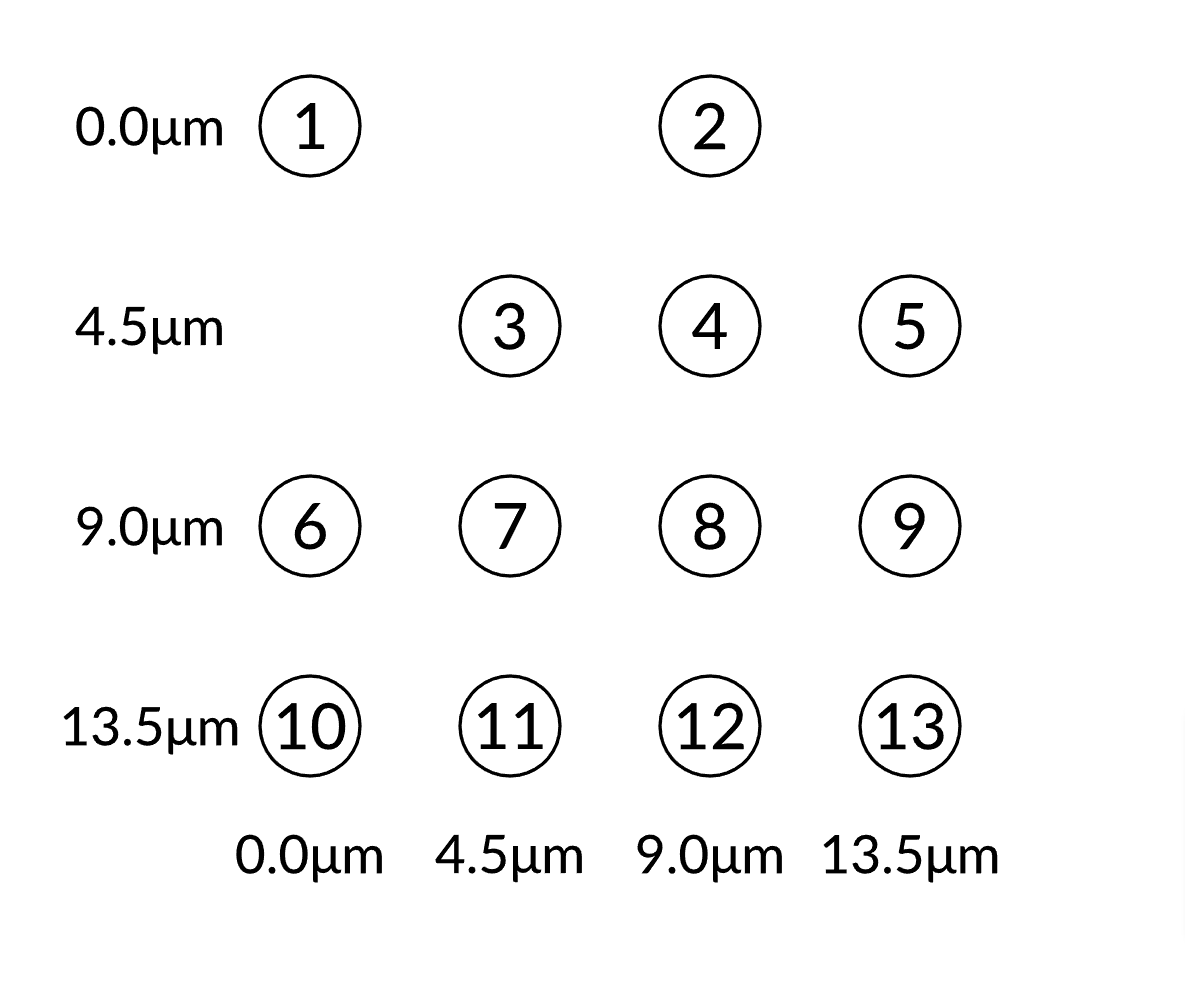
こうなりました。次にブロッケード半径を指定します。
Bloqade.plot(atoms, blockade_radius = 7.5)
そしてグラフを見ると、ブロッケード半径内に入っていない原子同士はつながりがありません。これはわかりやすいですね。影響範囲の及ぶところだけをグラフとして記述します。
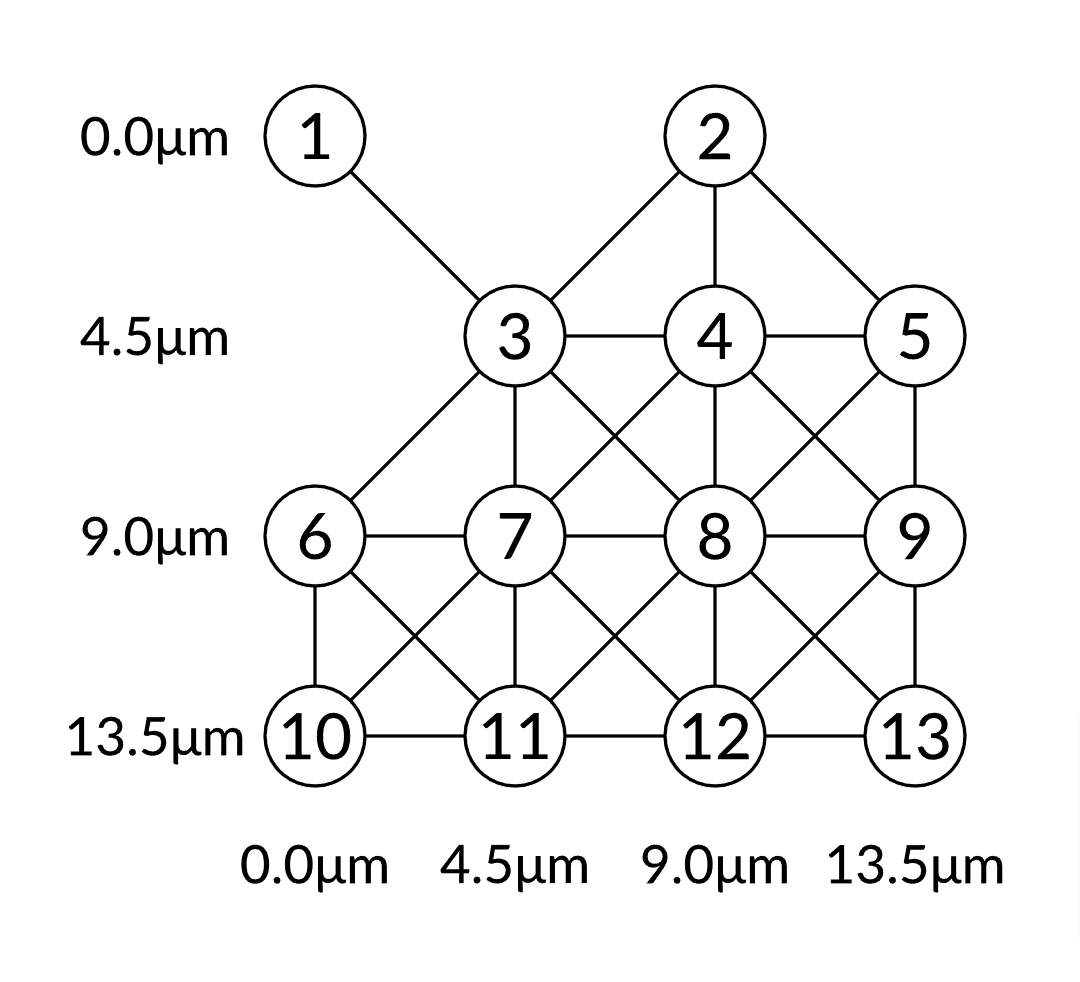
次に、古典ソルバーという現在のコンピュータの解き方で答えを見てみます。MISのこたえは4量子ビットと出ました。最終的に4量子ビットが隣り合わないかずは4が最大のようです。
graph = BloqadeMIS.unit_disk_graph(atoms, 7.5)
mis_size_and_counting = GenericTensorNetworks.solve(IndependentSet(graph), CountingMax())[]
(4.0, 26.0)ₜ
早速最初はアナログで解きます。スケジュールは以前見たようなスケジュールです。
T_max = 0.6
Ω_max = 2π * 4
Ω = piecewise_linear(clocks = [0.0, 0.1, 0.5, T_max], values = [0.0, Ω_max, Ω_max, 0])
Δ_start = -2π * 13
Δ_end = 2π * 11
Δ = piecewise_linear(clocks = [0.0, 0.1, 0.5, T_max], values = [Δ_start, Δ_start, Δ_end, Δ_end])
fig, (ax1, ax2) = plt.subplots(ncols = 2, figsize = (12, 4))
Bloqade.plot!(ax1, Ω)
ax1.set_ylabel("Ω/2π (MHz)")
Bloqade.plot!(ax2, Δ)
ax2.set_ylabel("Δ/2π (MHz)")
fig
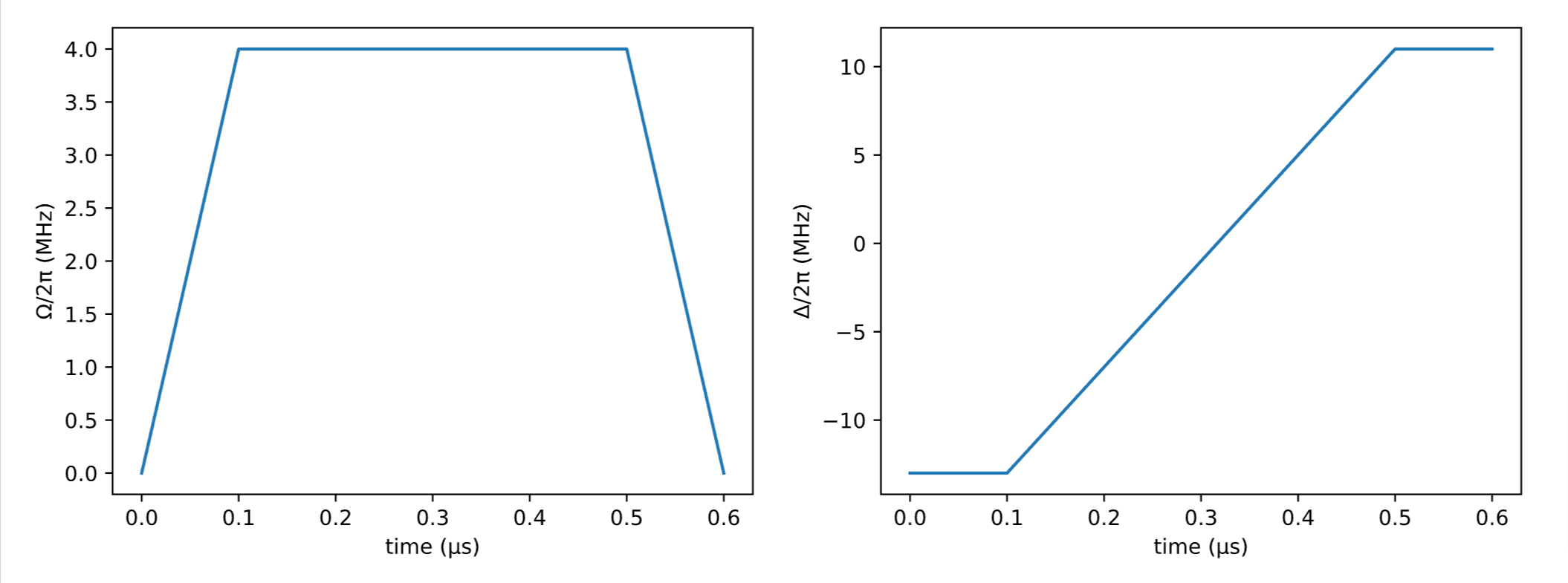
横磁場は一定で、リュードベリ状態の操作は線形でマイナスからプラスへ増やします。
hamiltonian = rydberg_h(atoms; Ω = Ω, Δ = Δ)
prob = SchrodingerProblem(zero_state(nqubits(hamiltonian)), T_max, hamiltonian)
emulate!(prob)
SchrodingerProblem:
register info:
type: YaoArrayRegister.ArrayReg{2, ComplexF64, Matrix{ComplexF64}}
storage size: 8 bytes
time span (μs): (0.0, 0.6)
equation:
storage size: 1.688 MiB
expression:
nqubits: 13
+
├─ [+] ∑ 2π ⋅ 8.627e5.0/|r_i-r_j|^6 n_i n_j
├─ [+] Ω(t) ⋅ ∑ σ^x_i
└─ [-] Δ(t) ⋅ ∑ n_i
options:
save_everystep: false
save_start: false
save_on: false
dense: false
bitstring_hist(prob.reg; nlargest = 20)
結果を見てみると、
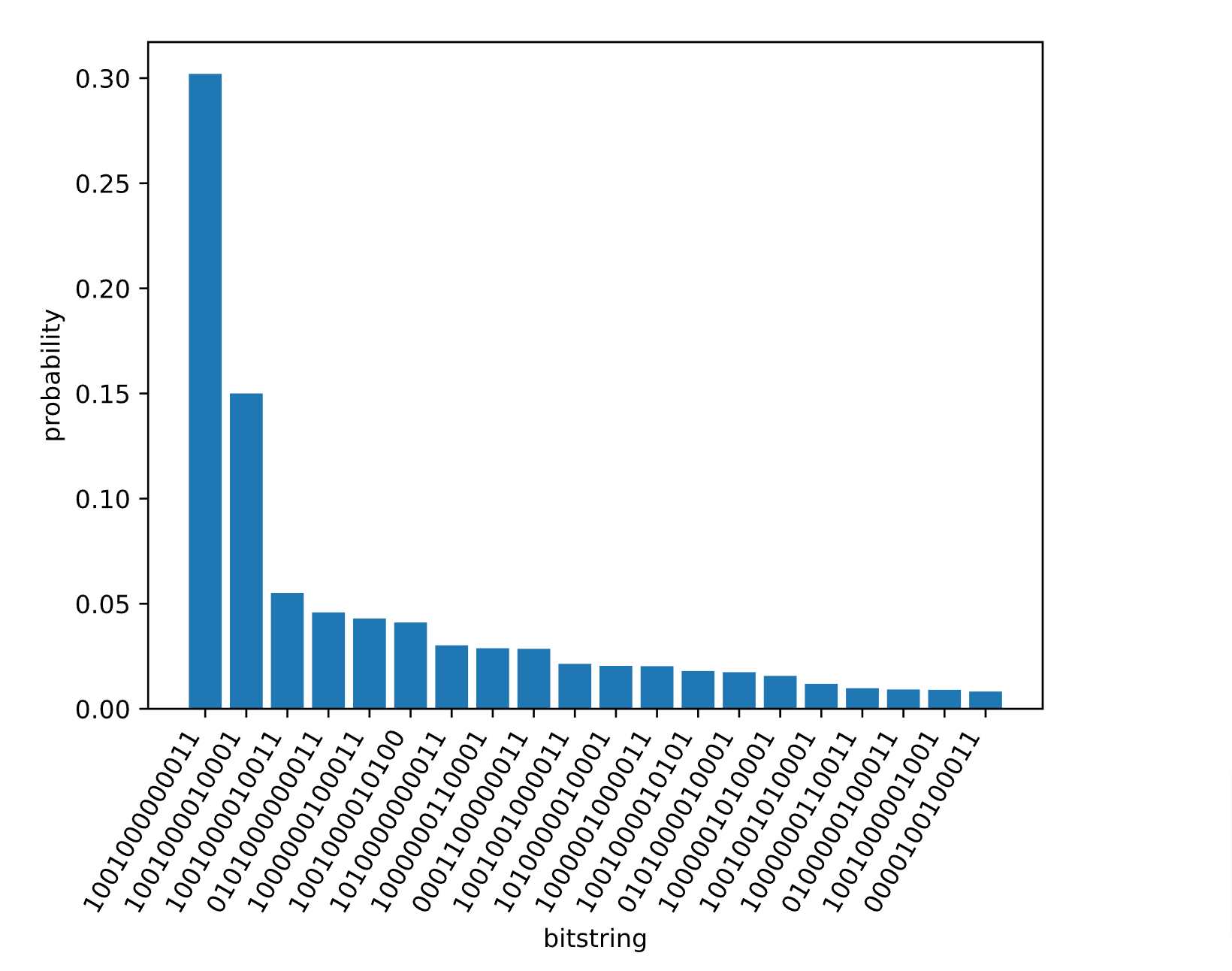
こんな感じで解けていました。グラフにも図示してみます。
best_bit_strings = most_probable(prob.reg, 2)
all_optimal_configs = GenericTensorNetworks.solve(IndependentSet(graph), ConfigsMax())[]
@assert all(bs -> GenericTensorNetworks.StaticBitVector([bs...]) ∈ all_optimal_configs.c, best_bit_strings)
Bloqade.plot(atoms, blockade_radius = 7.5; colors = [iszero(b) ? "white" : "red" for b in best_bit_strings[1]])
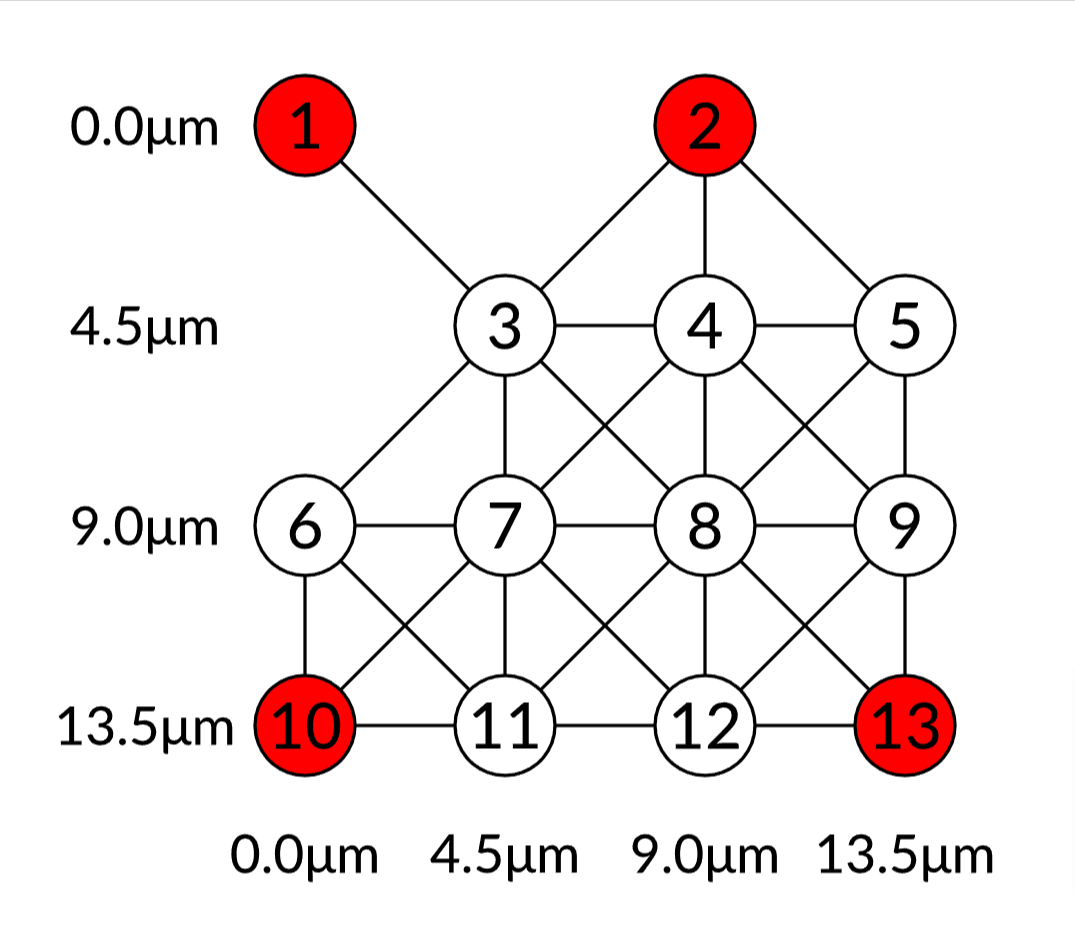
解けているのが確認できました。こちらのアナログシミュレーションは比較的成績がいいです。
QAOA
次にデジタル断熱計算をしてみます。QAOAはハミルトニアンを交互にかけて、そのかける時間の長さを最適化します。
使うハミルトニアンは二種類で一つは解きたい問題です。
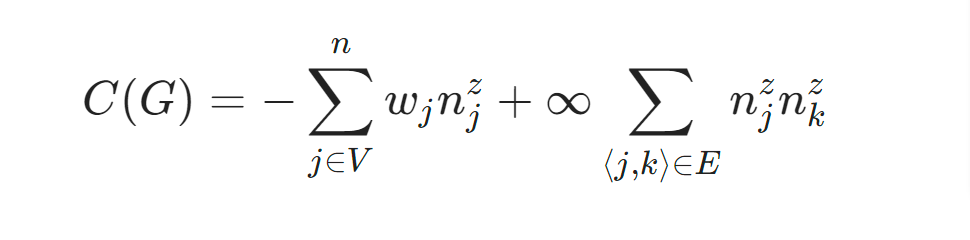
そうしてもう一つは自明な簡単な問題ですが、
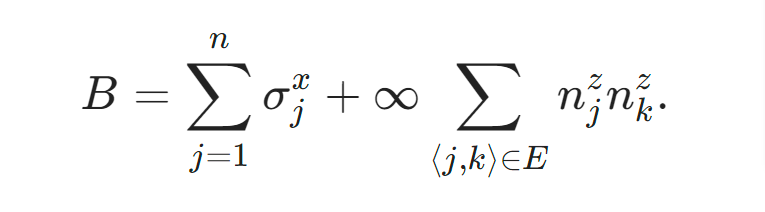
通常はΔXのみを使いますが、リュードベリ量子シミュレータの場合には相互作用が固定で入るのが特徴です。こちらは除くことができません。
スケジュールはガンマとデルタの値を離散的に変化させることで実現できるようです。
durations = fill(0.1, 6)
clocks = [0, cumsum(durations)...]
Ω2 = piecewise_constant(; clocks = clocks, values = repeat([Ω_max, 0.0], 3))
Δ2 = piecewise_constant(; clocks = clocks, values = repeat([0.0, Δ_end], 3))
fig, (ax1, ax2) = plt.subplots(ncols = 2, figsize = (12, 4))
Bloqade.plot!(ax1, Ω2)
ax1.set_ylabel("Ω/2π (MHz)")
Bloqade.plot!(ax2, Δ2)
ax2.set_ylabel("Δ/2π (MHz)")
fig
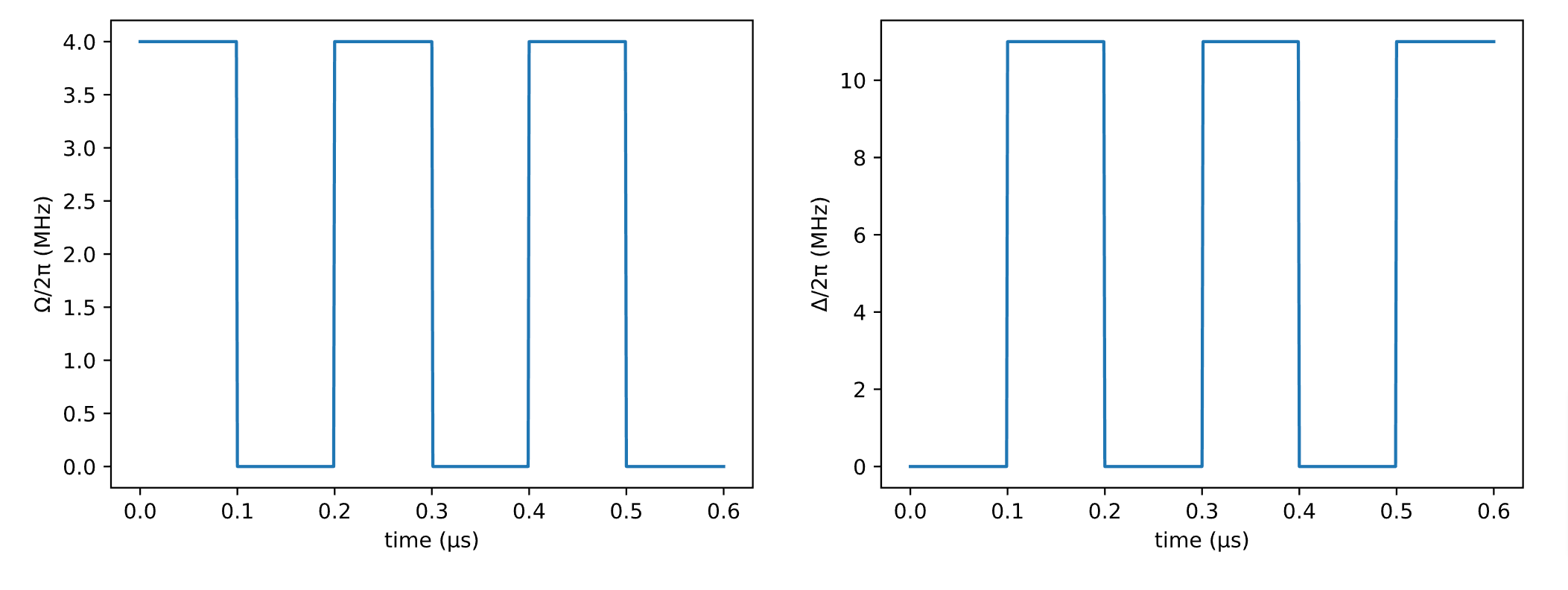
今回最小化したい答えは、最大独立集合問題なので、その答えにマイナスをつけたものを最小化します。その期待値を求めています。
hamiltonian2 = rydberg_h(atoms; Ω = Ω2, Δ = Δ2)
nsites = length(atoms)
subspace = blockade_subspace(atoms, 7.5) # we run our simulation within the blockade subspace
prob2 = KrylovEvolution(zero_state(subspace), clocks, hamiltonian2)
emulate!(prob2);
loss_MIS(reg) = -rydberg_density_sum(prob2.reg)
loss_MIS(prob2.reg)
-2.5628869128026794
function loss_piecewise_constant(atoms::AtomList, x::AbstractVector{T}) where {T}
@assert length(x) % 2 == 0
Ω_max = 4 * 2π
Δ_end = 11 * 2π
p = length(x) ÷ 2
# detuning and rabi terms
durations = abs.(x) # the durations of each layer of the QAOA pulse take the optimizing vector x as their input
clocks = \[0, cumsum(durations)...\]
Ωs = piecewise\_constant(; clocks = clocks, values = repeat(T\[Ω\_max, 0.0\], p))
Δs = piecewise\_constant(; clocks = clocks, values = repeat(T\[0.0, Δ\_end\], p))
hamiltonian = rydberg\_h(atoms; Ω = Ωs, Δ = Δs)
subspace = blockade\_subspace(atoms, 7.5) # we run our simulation within the blockade subspace
prob = KrylovEvolution(zero\_state(Complex{T}, subspace), clocks, hamiltonian)
emulate!(prob)
return -rydberg\_density\_sum(prob.reg), prob.reg
end
loss_piecewise_constant (generic function with 1 method)
x0 = durations
rydberg_density, reg1 = loss_piecewise_constant(atoms, x0)
rydberg_density
-2.5628869128026794
bitstring_hist(reg1; nlargest = 20)
それでは、初期のまだ最適化していない状態を見ます。
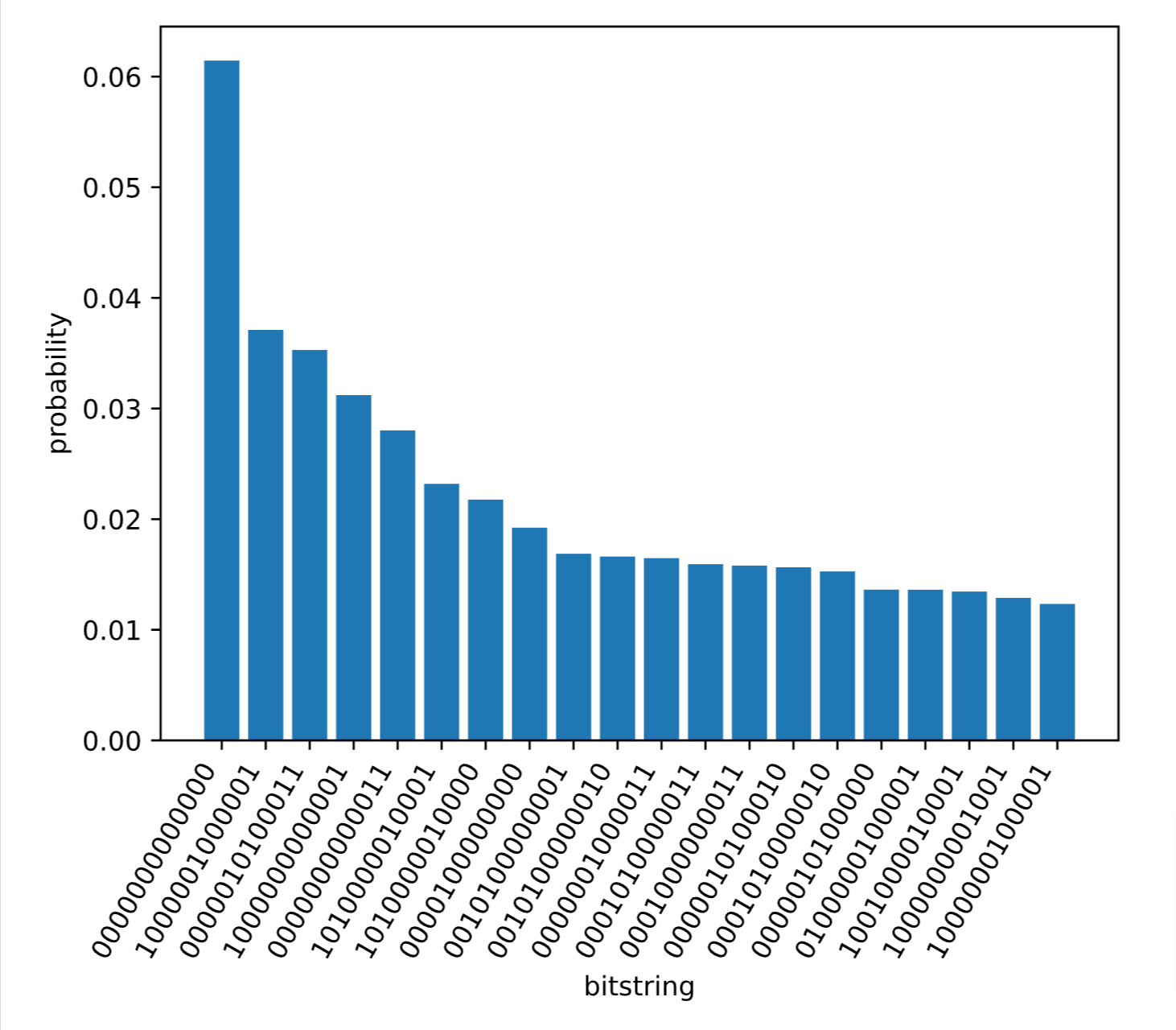
0の配列が見れます。次に最適化します。最適化されていないので最大独立集合の問題は初期状態では解けていません。
optresult = Optim.optimize(x -> loss_piecewise_constant(atoms, x)[1], x0)
rydberg_density_final, reg1_final = loss_piecewise_constant(atoms, optresult.minimizer)
rydberg_density_final
-3.0965910260012173
bitstring_hist(reg1_final; nlargest = 20)
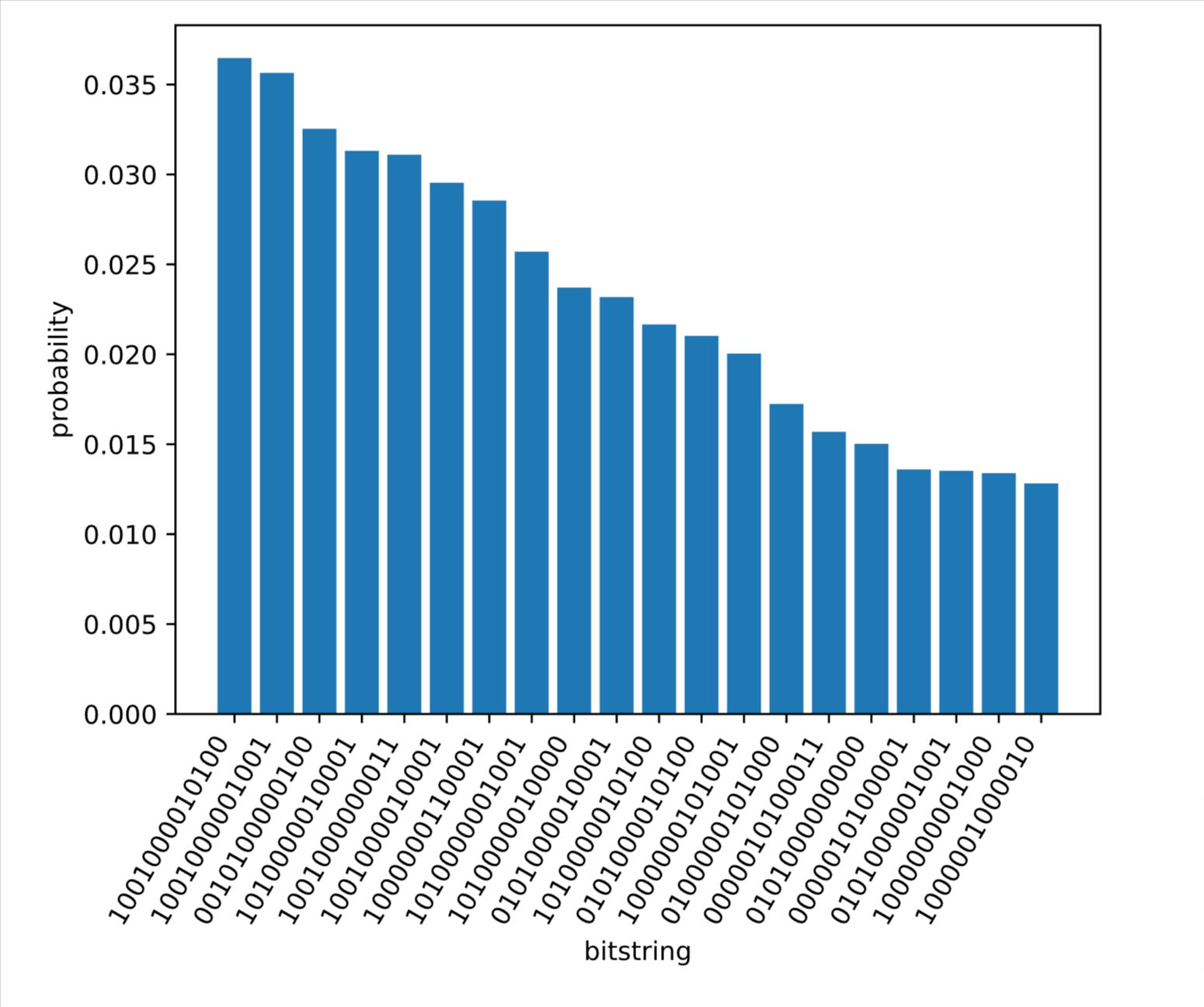
答えが最適化され、ある程度解けるようになりました。しかし、確率を見てみると比較的どの答えも確率が近くなっているため、結構微妙なラインな気がします。見た感じQAOAはうまくいっていますが、確実に解を求めたい場合にはアナログのほうが正解にたどり着くのは確実な気がします。それか、QAOAは特定の解を増やさず全体的にいい答えが出ているともとらえられる気がします。
以上です。
