ブログに下書き機能がないため、ちょっとずつ書いていきます。執筆中。

こんにちは、格子問題を利用した素因数分解のステップを確認します。

論文はこちらです。

Factoring integers with sublinear resources on a superconducting quantum processor

https://arxiv.org/abs/2212.12372

引用：https://arxiv.org/pdf/2212.12372.pdf

基本は量子古典ハイブリッドを利用し、QAOAをSchnorrの素因数分解アルゴリズムへ応用しています。フローは、事前準備として素因数分解したい整数Nから最初は格子上のCVP問題に落とし込みます。そこからBabaiのアルゴリズムを通じて得られるベクトルに関してより良い解を最適化問題で得ることによって、CVP問題の解を改善できるとおいうもので、それによってSchnorrのアルゴリズムを改善でき、最終的に素数のpとqを出力することができるというものです。

数学が苦手なので中身はよくわかりませんが、天下り式に計算ステップは確認できそうなのでざっくりコスト関数までの導出を見てみます。

論文では、3量子ビット、5量子ビット、10量子ビットのパターンを実行していますが、5と10量子ビットは論文の検証に時間がかかっているので今回は3量子ビットのパターンを検証します。5と10量子ビットは終わり次第ブログします（たぶん）。

最初に格子とターゲットベクトルを設定するところから始まるようです。

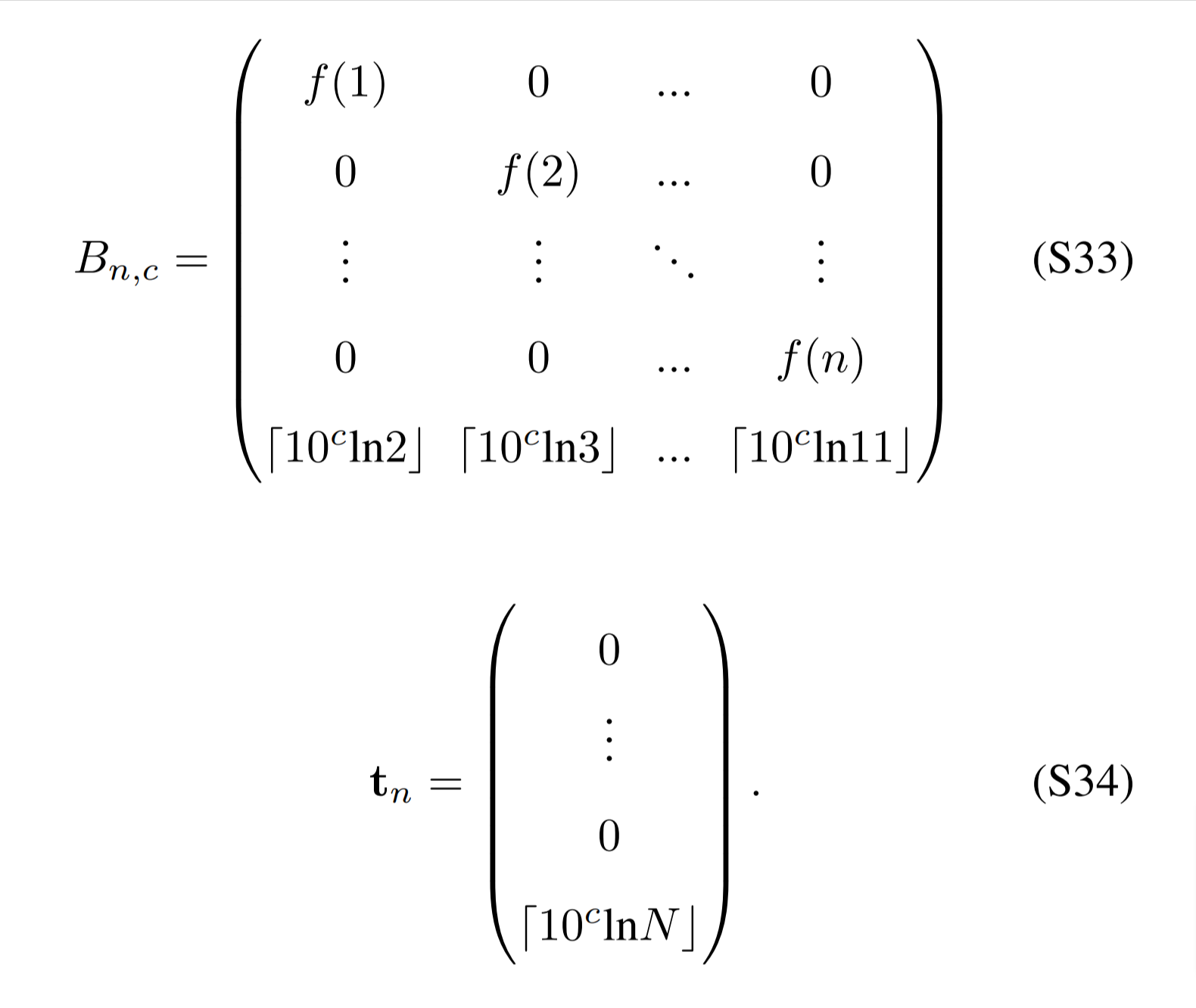
引用：https://arxiv.org/pdf/2212.12372.pdf

5量子ビットの例が載っていて、N=48567227の値に対して必要な格子の次元は、logN/loglogN らしいですので、

N = 48567227

import math
math.log2(N)/math.log2(math.log2(N))

#=>5.462503482939744

次元は5でよいようです。その他は3と10でした。なので、素数を前から順番に選ぶみたいで、10量子ビットも計算できるように10個選びました。

n = [2,3,5,7,11,13,17,19,23,29]

を使うようですね。次に格子を作るためのランダムの数を決めるのに、オリジナルの√lnpiの代わりに、[i/2]を使うことと、weightにN^cをつかうかわりに10^cをつかうとあります。cはなんか精度パラメータのようです。

fはランダムに配列を並べ替えるようです。ベースの配列の集合は先ほどの[i/2]を使うようで、

{1/2, 2/2, 3/2, 4/2, 5/2} = {1,1,2,2,3}

になります。ただ、論文中では、10量子ビットの場合には、

[1, 1, 1, 1, 2, 2, 2, 3, 3, 3]

i/4が使われているようです。

後は、精度パラメータcは1.5, 4, 4が利用されてました。

c3 = 1.5
c5 = 4
c10 = 4

あとは、それぞれの場合に上の式を使って格子とターゲットベクトルを作ります。本来シャッフルしますが、論文の検証をするために論文の並びに合わせてあります。

import random
import numpy as np

c3 = 1.5
c5 = 4
c10 = 4

n = [2,3,5,7,11,13,17,19,23,29]

N3 = 1961
N5 = 48567227
N10 = 261980999226229

#random.shuffle(l3)
#random.shuffle(l5)
#random.shuffle(l10)

l3 = [1,1,2]
l5 = [2,1,3,2,1]
l10 = [3,2,3,1,1,3,1,1,2,2]

B3 = np.diag(l3)
B3 = np.vstack((B3, [round(10**c5*math.log(i)) for i in n[:3]]))
print("B3")
print(B3)
print()
t3 = [0 for _ in range(4)]
t3[-1] = round(10**c3*math.log(N3))
print("t3")
print(t3)
print()

B5 = np.diag(l5)
B5 = np.vstack((B5, [round(10**c5*math.log(i)) for i in n[:5]]))
print("B5")
print(B5)
print()
t5 = [0 for _ in range(6)]
t5[-1] = round(10**c5*math.log(N5))
print("t5")
print(t5)
print()

B10 = np.diag(l10)
B10 = np.vstack((B10, [round(10**c5*math.log(i)) for i in n[:10]]))
print("B10")
print(B10)
print()
t10 = [0 for _ in range(11)]
t10[-1] = round(10**c10*math.log(N10))
print("t10")
print(t10)
print()

こちらを実行すると、

B3
[[ 1 0 0]
[ 0 1 0]
[ 0 0 2]
[22 35 51]]

t3
[0, 0, 0, 240]

B5
[[ 2 0 0 0 0]
[ 0 1 0 0 0]
[ 0 0 3 0 0]
[ 0 0 0 2 0]
[ 0 0 0 0 1]
[ 6931 10986 16094 19459 23979]]

t5
[0, 0, 0, 0, 0, 176985]

B10
[[ 3 0 0 0 0 0 0 0 0 0]
[ 0 2 0 0 0 0 0 0 0 0]
[ 0 0 3 0 0 0 0 0 0 0]
[ 0 0 0 1 0 0 0 0 0 0]
[ 0 0 0 0 1 0 0 0 0 0]
[ 0 0 0 0 0 3 0 0 0 0]
[ 0 0 0 0 0 0 1 0 0 0]
[ 0 0 0 0 0 0 0 1 0 0]
[ 0 0 0 0 0 0 0 0 2 0]
[ 0 0 0 0 0 0 0 0 0 2]
[ 6931 10986 16094 19459 23979 25649 28332 29444 31355 33673]]

t10
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 331993]

論文と同じになったことが確認できました。

これからLLLアルゴリズムをかけて、Babaiのアルゴリズムにかけていきます。

LLLアルゴリズムはこちらを利用させていただきました。

https://github.com/mitsu1119/Lattice_Reduction/blob/master/LLL.py

import random
import time

<vs, ws>

def inner_product(vs, ws):
  res = 0
  for i in range(len(vs)):
    res += vs[i] * ws[i]
  return res

vs - ws

def vecminus(vs, ws):
  res = []
  for i in range(len(vs)):
    res.append(vs[i] - ws[i])
  return res

a * vs

def scalarMul(vs, a):
  res = []
  for i in range(len(vs)):
    res.append(vs[i] * a)
  return res

vs -> vs*

def gram_schmidt(vs):
  n = len(vs)
  res = [0] * n
  mus = [([1] * n) for i in range(n)]
  res[0] = vs[0]
  for i in range(1, n):
    v = vs[i]
    for j in range(i):
      mus[i][j] = inner_product(vs[i], res[j]) / inner_product(res[j], res[j])
      v = vecminus(v, scalarMul(res[j], mus[i][j]))
    res[i] = v
  return res, mus

def lll(bs):
  n = len(bs)
  bstars, mus = gram_schmidt(bs)
  norm_bstars = [0] * n
  for i in range(n):
    norm_bstars[i] = inner_product(bstars[i], bstars[i])
  delta = 3 / 4

k = 1
  while k < n:
    for j in reversed(range(k)):
      mu_kj = mus[k][j]
      if abs(mu_kj) > 0.5:
        q = round(mu_kj)
        bs[k] = vecminus(bs[k], scalarMul(bs[j], q))
        # bstars, mus = gram_schmidt(bs)
        for l in range(j + 1):
          mus[k][l] = mus[k][l] - q * mus[j][l]

if norm_bstars[k] >= (delta - mus[k][k - 1] ** 2) * norm_bstars[k - 1]:
      k += 1
    else:
      bs[k], bs[k - 1] = bs[k - 1], bs[k]
      mup = mus[k][k - 1]
      B = norm_bstars[k] + (mup ** 2) * norm_bstars[k - 1]
      mus[k][k - 1] = mup * norm_bstars[k - 1] / B
      norm_bstars[k] = norm_bstars[k] * norm_bstars[k - 1] / B
      norm_bstars[k - 1] = B
      for j in range(k - 1):
        mus[k - 1][j], mus[k][j] = mus[k][j], mus[k - 1][j]
      for j in range(k + 1, n):
        t = mus[j][k]
        mus[j][k] = mus[j][k - 1] - mup * t
        mus[j][k - 1] = t + mus[k][k - 1] * mus[j][k]
      k = max(k - 1, 1)
  return [list(map(int, b)) for b in bs]

こちらでやってみると、

B3_vs = np.copy(B3.T).tolist()
B3_lll = np.array(lll(B3_vs)).T
print(B3_lll)

[[ 1 -3 -4]
[-2 2 1]
[ 2 0 2]
[ 3 4 -2]]

なんか列の順番は違いますが、答えは出ています。B5は、

B5_vs = np.copy(B5.T).tolist()
B5_lll = np.array(lll(B5_vs)).T
print(B5_lll)

[[ 6 -8 -4 2 -4]
[ -4 -3 -5 11 -3]
[ 6 6 0 3 -3]
[ 4 -2 12 0 4]
[ -2 2 -2 -6 1]
[ -3 5 4 -3 -17]]

なんか順番が、、、この後はさらに5量子ビットと10量子ビットは全然わからなくなったので、3量子ビットで進めます。Babaiのアルゴリズムの続きはそのうち調べるとして、ちょっと飛ばしてBabaiを実行した後は、論文からは下記の行列とベクトルが得られますので、

D3 = [[1, -4, -3],[-2, 1, 2],[2, 2, 0],[3, -2, 4]]
t3h = [0, 4, 4, 2]

処理されたあとの情報です。Dとtが得られました。（本当は自分で手作業でやってみたいところですがまだ時間がかかりそうなので割愛します）

ここから、各行を使って連立方程式を作り、それぞれの行を二乗してたしあわせ、最小化問題に落とし込みます。

import sympy

sympy.var('x1 x2 x3')

#make QUBO from D3 and t3h
h3 = 0
for i in range(4):
  h3 += (D3[i][0]*x1 + D3[i][1]*x2 + D3[i][2]*x3 - t3h[i])**2

#expand and subs
h3e = sympy.expand(h3)
h3e = h3e.subs([(x1**2, x1), (x2**2, x2), (x3**2, x3)])
print(h3e)

上記は式を展開し、01バイナリ値から、単項の二乗の項を0^2=0, 1^2=1のルールを適用しています。

-16*x1*x2 + 10*x1*x3 + 6*x1 + 12*x2*x3 + 9*x2 - 3*x3 + 36

最後にバイナリ値をpauliZに書き換えます。cとμの値によって符号が変わるので、

sympy.var('z1 z2 z3')

#transform QUBO to PauliZ
h3e = h3e.subs([(x1, 0.5-0.5*z1), (x2, 0.5-0.5*z2), (x3, 0.5-0.5*z3)])
h3e = sympy.expand(h3e)
print(h3e)

こうすると、

-4.0*z1*z2 + 2.5*z1*z3 - 1.5*z1 + 3.0*z2*z3 - 3.5*z2 - 4.0*z3 + 43.5

論文の通りになりました。（ちょっと符号とか怪しいですが）

後は、以前の記事で紹介したGUIでのQAOAからいれるか、

[レビュー]中国の暗号解読論文の3量子ビットの場合のコスト関数をQAOAで解いてみる

https://blueqat.com/yuichiro_minato2/d0d6fba3-2169-4833-97f9-c79ef85af7da

blueqatを使って、

from blueqat import Circuit
from blueqat.utils import qaoa
from blueqat.pauli import qubo_bit as q
from blueqat.pauli import X,Y,Z,I

hamiltonian = -4*Z(0)*Z(1)+2.5*Z(0)*Z(2)-1.5*Z(0)+3*Z(1)*Z(2)-3.5*Z(1)-4*Z(2)
step = 3

result = qaoa(hamiltonian, step)
d = result.circuit.run(shots=1000)

from matplotlib import pyplot as plt
plt.bar(d.keys(), d.values())
plt.show()

できました。

つづく